题目一：斐波那契数列问题的递归和动态规划

【题目】

给定整数 N，返回斐波那契数列的第 N 项。

补充问题 1： 给定整数 N，代表台阶数，一次可以跨 2 个或者 1 个台阶，返回有多少种走法。

补充问题 2： 假设农场中成熟的母牛每年只会生 1 头小母牛，并且永远不会死。第一年农场有 1 只成熟的母牛，从第二年开始，母牛开始生小母牛。每只小母牛 3 年之后成熟又可以生小母牛。给定整数 N，求出 N 年后牛的数量。

【举例】

补充问题1：

N=3， 可以三次都跨 1 个台阶；也可以先跨 2 个台阶，再跨 1 个台阶；还可以先跨 1 个台阶，再跨 2 个台阶。所以有三种走法，返回 3。

补充问题2：

N=6， 第 1 年 1 头成熟母牛记为 a； 第 2 年 a 生了新的小母牛， 记为 b，总牛数为 2； 第 3年 a 生了新的小母牛， 记为 c，总牛数为 3； 第 4 年 a 生了新的小母牛， 记为 d，总牛数为 4。第 5 年 b 成熟了， a 和 b 分别生了新的小母牛，总牛数为 6； 第 6 年 c也成熟了， a、 b 和 c 分别生了新的小母牛，总牛数为 9， 返回 9。

【要求】

对于以上的所有问题，请实现复杂度为O(logN)的解法。

【难度】

【解答】

原问题。 O($2^n$)的方法。斐波那契数列为 1， 1， 2， 3， 5， 8，…，也就是除第 1 项和第 2 项为 1 以外，对于第 N 项，有 F(N)=F(N-1)+F(N-2)，于是很轻松地写出暴力递归的代码。请参看如下代码中的 f1 方法。 

1
2
3
4
5
6
7
8
9
public int f1(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return 1;
    }
    return f1(n-1) + f1(n-2);
}

O(N)的方法。斐波那契数列可以从左到右依次求出每一项的值，那么通过顺序计算求到第 N 项即可。请参看如下代码中的 f2 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int f2(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return 1;
    }
    int res = 1;
    int pre = 1;
    int temp = 0;
    for (int i = 3; i <= n; i++) {
        temp = res;
        res = res + pre;
        pre = temp;
    }
    return res;
}

O(logN)的方法。如果递归式严格遵循 F(N)=F(N-1)+F(N-2)，对于求第 N 项的值，有矩阵乘法的方式可以将时间复杂度降至 O(logN)。F(n)=F(n-1)+F(n-2)，是一个二阶递推数列，一定可以用矩阵乘法的形式表示，且状态矩阵为 2×2 的矩阵：

$$ (F(n),F(n-1))=(F(n-1),F(n-2))× \begin{vmatrix}a&b \\ c&d \ \end{vmatrix} $$

把斐波那契数列的前 4 项 F(1)=1， F(2)=1， F(3)=2， F(4)=3 代入，可以求出状态矩阵：

$$ \begin{vmatrix}a&b \\ c&d \ \end{vmatrix} =\begin{vmatrix}1&1 \\ 1&0 \ \end{vmatrix}$$

求矩阵之后，当 n>2 时，原来的公式可化简为：

$$ (F(3),F(2))=(F(2),F(1))× \begin{vmatrix}1&1 \\ 1&0 \ \end{vmatrix}=(1,1)× \begin{vmatrix} 1&1 \\ 1&0 \end{vmatrix}$$​

$$ (F(4),F(3))=(F(3),F(2))× \begin{vmatrix}1&1 \\ 1&0 \ \end{vmatrix}=(1,1)× {\begin{vmatrix} 1&1 \\ 1&0 \end{vmatrix}}^2$$

$$ \vdots $$

$$ (F(n),F(n-1))=(F(n-1),F(n-2))× \begin{vmatrix}1&1 \\ 1&0 \ \end{vmatrix}=(1,1)× {\begin{vmatrix} 1&1 \\ 1&0 \end{vmatrix}}^{n-2}$$

所以， 求斐波那契数列第 N 项的问题就变成了如何用最快的方法求一个矩阵 N 次方的问题，而求矩阵 N 次方的问题明显是一个能够在 O(logN)时间内解决的问题。为了表述方便，我们现在用求一个整数 N 次方的例子来说明，因为只要理解了如何在O(logN)的时间复杂度内求整数 N次方的问题，对于求矩阵 N 次方的问题是同理的，区别是矩阵乘法和整数乘法在细节上有些不一样，但对于怎么乘更快，两者的道理相同。

假设一个整数是 10，如何最快地求解 10 的 75 次方。

1． 75 的二进制数形式为 1001011。

2． 10 的 75 次方=1064×108×102×101。

在这个过程中，我们先求出 101，然后根据 101求出 102，再根据 102求出 104， ……，最后根据 1032 求出 1064，即 75的二进制数形式总共有多少位，我们就使用了几次乘法。

3．在步骤 2 进行的过程中， 把应该累乘的值相乘即可，比如 1064、 108、 102、 101 应该累乘，因为 64、 8、 2、 1对应到 75 的二进制数中，相应的位上是 1；而 1032、 1016、 104不应该累乘，因为 32、 16、 4 对应到 75 的二进制数中，相应的位上是 0。

对矩阵来说同理，求矩阵 m 的 p 次方请参看如下代码中的 matrixPower 方法。其中 muliMatrix方法是两个矩阵相乘的具体实现。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public int[][] muliMatrix(int[][] m1, int[][] m2) {
    int[][] res = new int[m1.length][m2[0].length];
    for (int i = 0; i < m1.length; i++) {
        for (int j = 0; j < m2[0].length; j++) {
            int ans = 0;
            for (int k = 0; k < m1[i].length; k++) {
                ans += m1[i][k] * m2[k][j];
            }
            res[i][j] = ans;
        }
    }
}

public int[][] matrixPower(int[][] m, int p) {
    int[][] res = new int[m.length][m[0].length];
    for (int i = 0; i < m.length; i++) {
        res[i][i] = 1;
    }
    int[][] temp = m;
    for (; p != 0; p >>= 1) {
        if ((p & 1) != 0) {
            res = muliMatrix(res, temp);
        }
        temp = muliMatrix(temp, temp);
    }
    return res;
}

用矩阵乘法求解斐波那契数列第 N 项的全部过程请参看如下代码中的 f3 方法。 

1
2
3
4
5
6
7
8
9
10
11
public int f3(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return 1;
    }
    int[][] base = {{1, ,1}, {1, 0}};
    int[][] res = matrixPower(base, n-2);
    return res[0][0] + res[1][0];
}

补充问题 1: 如果台阶只有 1 级，方法只有 1 种。如果台阶有 2 级，方法有 2 种。如果台阶有 N 级，最后跳上第 N 级的情况，要么是从 N-2 级台阶直接跨 2 级台阶，要么是从 N-1 级台阶跨 1 级台阶，所以台阶有 N 级的方法数为跨到 N-2 级台阶的方法数加上跨到 N-1 级台阶的方法数，即 S(N)=S(N-1)+S(N-2)，初始项 S(1)=1， S(2)=2。 所以， 类似斐波那契数列，唯一的不同就是初始项不同。可以很轻易地写出 O(2N)与 O(N)的方法，请参看如下代码中的 s1 和 s2 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public int s1(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return n;
    }
    return s1(n-1) + s1(n-2);
}

public int s2(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n==2) {
        return n;
    }
    int res = 2;
    int pre = 1;
    int temp = 0;
    for (int i = 3; i <= n; i++) {
        temp = res;
        res = res + pre;
        pre = temp;
    }
    return res;
}

O(logN)的方法。表达式 S(n)=S(n-1)+S(n-2)是一个二阶递推数列，同样， 用上文矩阵乘法的方法，根据前 4 项 S(1)=1， S(2)=2， S(3)=3， S(4)=5， 求出状态矩阵：

$$\begin{vmatrix} a&b \\ c&d \end{vmatrix} = \begin{vmatrix} 1&1 \\ 1&0 \end{vmatrix} $$

同样根据上文的过程得到：

$$ (S(n), S(n-1))=(S(2) - S(1))\times {\begin{vmatrix}1&1\\ 1&0 \end{vmatrix}}^{n-2} = (2,1)\times {\begin{vmatrix}1&1\\ 1&0 \end{vmatrix}}^{n-2} $$

全部实现请参考下面代码中的s3方法。

1
2
3
4
5
6
7
8
9
10
11
public int s3(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return n;
    }
    int[][] base = {{1,1},{1,0}};
    int[][] res = matrixPower(base, n-2);
    return 2 * res[0][0] + res[1][0];
}

补充问题 2。所有的牛都不会死，所以第 N-1 年的牛会毫无损失地活到第 N 年。同时所有成熟的牛都会生 1 头新的牛，那么成熟牛的数量如何估计？就是第 N-3 年的所有牛，到第 N 年肯定都是成熟的牛，其间出生的牛肯定都没有成熟。所以C(n)=C(n-1)+C(n-3)，初始项为 C(1)=1，C(2)=2， C(3)=3。这个和斐波那契数列又十分类似，只不过 C(n)依赖 C(n-1)和 C(n-3)的值，而斐波那契数列 F(n)依赖 F(n-1)和 F(n-2)的值。同样可以轻易地写出 O(2N)与 O(N)的方法，请参看如下代码中的 c1 和 c2 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public int c1(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2 || n == 3) {
        return n;
    }
    return c1(n-1) + c1(n-3);
}

public int c2(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2 || n == 3) {
        return n;
    }
    int res = 3;
    int pre = 2;
    int prepre = 1;
    int temp = 0;
    for (int i = 4; i <= n; i++) {
        temp = res;
        res = res + prepre;
        prepre = pre;
        pre = temp;
    }
    return res;
}

O(logN)的方法。 C(n)=C(n-1)+C(n-3)是一个三阶递推数列，一定可以用矩阵乘法的形式表示，且状态矩阵为 3×3 的矩阵。

$$ (C_n, C_{n-1},C_{n-2}) = (C_{n-1}, C_{n-2},C_{n-3}) \times \begin{vmatrix} a&b&c \\ d&e&f \\ g&h&j \end{vmatrix}$$

把前 5 项 C(1)=1， C(2)=2， C(3)=3， C(4)=4， C(5)=6 代入，求出状态矩阵：

$$ \begin{vmatrix} a&b&c \\ d&e&f \\ g&h&j \end{vmatrix} = \begin{vmatrix} 1&1&0 \\ 0&0&1 \\ 1&0&0 \end{vmatrix} $$

求矩阵之后，当 n>3 时，原来的公式可化简为：

$$ (C_n, C_{n-1},C_{n-2}) = (C_3, C_2,C_1) \times {\begin{vmatrix} 1&1&0 \\ 0&0&1 \\ 1&0&0 \end{vmatrix}}^{n-3} = (3,2,1) \times {\begin{vmatrix} 1&1&0 \\ 0&0&1 \\ 1&0&0 \end{vmatrix}}^{n-3}$$

接下来的过程又是利用加速矩阵乘法的方式进行实现，具体请参看如下代码中的 c3 方法。 

1
2
3
4
5
6
7
8
9
10
11
public int c3(int n) {
    if (n < 1) {
        return 0;
    }
    if (n == 1 || n == 2 || n == 3) {
        return n;
    }
    int[][] base = {{1,1,0},{0,0,1},{1,0,0}};
    int[][] res = matrixPower(base, n - 3);
    return 3 * res[0][0] + 2 * res[1][0] + res[2][0];
}

如果递归式严格符合 F(n)=a×F(n-1)+b×F(n-2)+…+k×F(n-i)，那么它就是一个 i 阶的递推式，必然有与 i×i 的状态矩阵有关的矩阵乘法的表达。一律可以用加速矩阵乘法的动态规划将时间复杂度降为 O(logN)。

题目二：矩阵最小路径和

【题目】

给定一个矩阵 m，从左上角开始每次只能向右或者向下走，最后到达右下角的位置，路径上所有的数字累加起来就是路径和，返回所有的路径中最小的路径和。

【举例】

如果给定的m如下：

1 3 5 9

8 1 3 4

5 0 6 1

8 8 4 0

路径 1， 3， 1， 0， 6， 1， 0 是所有路径中路径和最小的，所以返回 12。

【难度】

【解答】

经典动态规划方法。假设矩阵 m 的大小为 M×N，行数为 M，列数为 N。先生成大小和 m一样的矩阵 dp， dp[i][j]的值表示从左上角（即(0,0)） 位置走到(i,j)位置的最小路径和。对 m 的第一行的所有位置来说， 即(0,j)（0≤ j<N），从(0,0)位置走到(0,j)位置只能向右走，所以(0,0)位置到(0,j)位置的路径和就是 m[0][0..j]这些值的累加结果。同理，对 m 的第一列的所有位置来说， 即(i,0)（0≤ i<M），从(0,0)位置走到(i,0)位置只能向下走，所以(0,0)位置到(i,0)位置的路径和就是 m[0..i][0]
这些值的累加结果。以题目中的例子来说， dp 第一行和第一列的值如下：

1 4 9 18

9

14

22

除第一行和第一列的其他位置（i,j） 外，都有左边位置（i-1,j） 和上边位置（i,j-1）。从（0,0）到（i,j） 的路径必然经过位置（i-1,j） 或位置（i,j-1），所以， dp[i][j]=min{dp[i-1][j],dp[i][j-1]}+m[i][j]，含义是比较从（0,0） 位置开始，经过（i-1,j） 位置最终到达（i,j） 的最小路径和经过（i,j-1） 位置最终到达（i,j） 的最小路径之间，哪条路径的路径和更小。 那么更小的路径和就是 dp[i][j]的值。以题目的例子来说，最终生成的 dp 矩阵如下：

1 4 9 18
9 5 8 12
14 5 11 12
22 13 15 12

除第一行和第一列外，每一个位置都考虑从左边到达自己的路径和更小还是从上边达到自己的路径和更小。最右下角的值就是整个问题的答案。具体过程请参看如下代码中的 minPathSum1 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int minPathSum1(int[][] m) {
    if (m == null || m.length == 0 || m[0] == null || m[0].length == null) {
        return 0;
    }
    int row = m.length;
    int col = m[0].length;
    int[][] dp = new int [row][col];
    dp[0][0] = m[0][0];
    for (int i = 1; i < row; i++) {
        dp[i][0] = dp[i-1][0] + m[i][0];
    }
    for (int j = 1; j < col; j++) {
        dp[0][j] = dp[0][j-1] + m[0][j];
    }
    for (int i = 1; i < row; i++) {
        for (int j = 1; j < col; j++) {
            dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + m[i][j];
        }
    }
    return dp[row-1][col-1];
}

矩阵中一共有 M×N 个位置，每个位置都计算一次从（0,0） 位置达到自己的最小路径和，计算的时候只是比较上边位置的最小路径和与左边位置的最小路径和哪个更小，所以时间复杂度为 O(M×N)， dp 矩阵的大小为 M×N， 所以额外空间复杂度为O(M×N)。

动态规划经过空间压缩后的方法。这道题的经典动态规划方法在经过空间压缩之后，时间复杂度依然是 O(M×N)，但是额外空间复杂度可以从 O(M×N)减小至 O(min{M,N})，也就是不使用大小为 M×N 的 dp 矩阵，而仅仅使用大小为 min{M,N}的 arr 数组。具体过程如下（以题目的例子来举例说明）。

1． 生成长度为 4 的数组 arr，初始时 arr=[0,0,0,0]，我们知道从（0,0） 位置到达 m 中第一行的每个位置，最小路径和就是从（0,0） 位置的值开始依次累加的结果，所以依次把 arr 设置为 arr=[1,4,9,18]，此时 arr[j]的值代表从（0,0） 位置达到(0,j)位置的最小路径和。

2． 步骤 1 中 arr[j]的值代表从（0,0） 位置达到（0,j） 位置的最小路径和，在这一步中想把arr[j]的值更新成从（0,0） 位置达到（1,j） 位置的最小路径和。首先来看 arr[0]，更新之前 arr[0]的值代表（0,0） 位置到达（0,0） 位置的最小路径和（dp[0][0]），如果想把 arr[0]更新成从（0,0）位置达到（1,0） 位置的最小路径和（dp[1][0]），令arr[0]=arr[0]+m[1][0]=9 即可。然后来看 arr[1]，更新之前 arr[1]的值代表（0,0） 位置到达（0,1） 位置的最小路径和（dp[0][1]），更新之后想让arr[1]代表（0,0） 位置到达（1,1） 位置的最小路径和（dp[1][1]）。根据动态规划的求解过程，到达（1,1） 位置有两种选择，一种是从（1,0） 位置到达（1,1） 位置（dp[1][0]+m[1][1]），另一种是从（0,1） 位置到达（1,1） 位置（dp[0][1]+m[1][1])），应该选择路径和最小的那个。此时 arr[0]的值已经更新成 dp[1][0]， arr[1]目前还没有更新，所以， arr[1]还是 dp[0][1]， arr[1]=min{arr[0],arr[1]}+m[1][1]=5。更新之后， arr[1]的值变为 dp[1][1]的值。同理， arr[2]=min{arr[1],arr[2]}+m[1][2]， ……
最终 arr 可以更新成[9,5,8,12]。

3． 重复步骤 2 的更新过程，一直到 arr 彻底变成 dp 矩阵的最后一行。整个过程其实就是不断滚动更新 arr 数组，让 arr 依次变成 dp 矩阵每一行的值，最终变成 dp 矩阵最后一行的值。

本题的例子是矩阵 m 的行数等于列数，如果给定的矩阵列数小于行数（N<M），依然可以用上面的方法令 arr 更新成 dp 矩阵每一行的值。但如果给定的矩阵行数小于列数（M<N），那么就生成长度为 M 的 arr，然后令 arr 更新成 dp 矩阵每一列的值，从左向右滚动过去。 以本例来说，如果按列来更新， arr 首先更新成[1,9,14,22]，然后向右滚动更新成[4,5,5,13]，继续向右滚动更新成[9,8,11,15]，最后是[18,12,12,12]。总之， 是根据给定矩阵行和列的大小关系决定滚动的方式，始终生成最小长度（min{M,N}）的 arr 数组。具体过程请参看如下代码中的 minPathSum2方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int minPathSum2(int[][] m) {
    if (m == null || m.length == 0 || m[0].length == 0 || m[0] == null) {
        return 0;
    }
    int more = Math.max(m.length, m[0].length);
    int less = Math.min(m.length, m[0].length);
    boolean rowmore = more == m.length;
    int[] arr = new int[less];
    arr[0] = m[0][0];
    for (int i = 1; i < less; i++) {
        arr[i] = arr[i-1] + (rowmore ? m[0][i] : m[i][0]);
    }
    for (int i = 1; i < more; i++) {
        arr[0] = arr[0] + (rowmore ? m[i][0] : m[0][i]);
        for (int j = 1; j < less; j++) {
            arr[j] = Math.min(arr[j-1], arr[j]) + (rowmore ? m[i][j] : m[j][i]);
        }
    }
    return arr[less - 1];
}

【扩展】

本题压缩空间的方法几乎可以应用到所有需要二维动态规划表的面试题目中，通过一个数组滚动更新的方式无疑节省了大量的空间。没有优化之前，取得某个位置动态规划值的过程是在矩阵中进行两次寻址，优化后， 这一过程只需要一次寻址，程序的常数时间也得到了一定程度的加速。但是空间压缩的方法是有局限性的，本题如果改成“打印具有最小路径和的路径”，那么就不能使用空间压缩的方法。如果类似本题这种需要二维表的动态规划题目，最终目的是想求最优解的具体路径，往往需要完整的动态规划表，但如果只是想求最优解的值，则可以使用空间压缩的方法。因为空间压缩的方法是滚动更新的，会覆盖之前求解的值，让求解轨迹变得不可回溯。希望读者好好研究这种空间压缩的实现技巧，本书还有许多动态规划题目会涉及空间压缩方法的实现。

题目三：换钱的最少货币数

【题目】

给定数组 arr， arr 中所有的值都为正数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张， 再给定一个整数 aim， 代表要找的钱数，求组成 aim 的最少货币数。

【举例】

arr=[5,2,3]， aim=20。
4 张 5 元可以组成 20 元，其他的找钱方案都要使用更多张的货币，所以返回 4。

arr=[5,2,3]， aim=0。
不用任何货币就可以组成 0 元，返回 0。

arr=[3,5]， aim=2。
根本无法组成 2 元，钱不能找开的情况下默认返回-1。

【难度】

【解答】

这道题我们使用暴力递归优化成动态规划的套路，不熟悉套路的读者请先阅读本书“机器人达到指定位置方法数”问题的解答。 先想暴力尝试的方法，然后优化成动态规划。首先是原问题的暴力尝试方法。只有想出尝试方法是最难、最重要的。

原问题的暴力尝试过程请看如下的 process 方法。 就是每一种面值都尝试不同的张数，尝试是从哪里开始的？是从 arr[0]开始依次往右考虑所有面值的，主方法见 minCoins1 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
public int minCoinsl(int[] arr, int aim) {
        if (arr == null || arr.length == 0 || aim < 0) {
            return -1;
        }
        return process(arr, 0, aim);
    }

    // 当前考虑的面值是arr[i],还剩rest的钱需要找零
    // 如果返回-1，说明自由使用arr[i...N-1]面值的情况下，无论如何也无法找零rest
    // 如果不是-1，代表自由使用arr[i...N-1]面值的情况下，找零rest需要的最少张数
    public int process(int[] arr, int i, int rest) {
        // base case:
        // 已经没有面值可以考虑了
        // 如果此时剩余的钱为0，返回0张
        // 如果此时剩余的钱不是0，返回-1
        if (i == arr.length) {
            return rest == 0 ? 0 : -1
        }
        // 最少张数，初始时为-1，因为还没有找到有效解
        int res = -1;
        // 依次尝试使用当前面值的（arr[i]）0张，1张，2张...但是总面值不能超过rest
        for (int k = 0; k * arr[i] <= rest; k++) {
            // 使用了k张arr[i], 剩下的钱为rest-arr[i]
            // 交给剩下的面值去搞定
            int next = process(arr, i + 1, rest - k * arr[i]);
            if (next != -1) {
                res = res == -1 ? next + k : Math.min(res, next + k);
                // 这一行代码很难理解
            }
        }
        return res;
    }

原问题暴力递归改动态规划，利用优化套路过程如下。

前提：尝试过程是无后效性的。上面的尝试其实明显是无后效性的，但是为了方便理解，我们还是举个例子， arr = {5,2,3,1}， aim=100，那么 process(arr,0,100)的返回值就是最终答案。如果使用 2 张 5 元， 0 张 2 元，那么后续的过程是 process(arr,2,90)；但如果使用 0 张 5 元， 5 张 2元，那么后续的过程还是 process(arr,2,90)。这个状态的返回值肯定是一样的，说明一个状态最终的返回值与怎么达到这个状态的过程无关。

1）可变参数 i 和 rest 一旦确定，返回值就确定了。

2） 如果可变参数 i 和 rest 组合的所有情况组成一张二维表，这张表一定可以装下所有的回值。i 的含义是 arr 中的位置，又因为 process 中允许 i 来到 arr 的终止位置，所以 i 的范围是[0,N]。rest 代表剩余的钱数，剩余的钱不可能大于 aim，所以 rest 的范围是[0,aim]。所以这张二维表是一个 N 行 aim 列的表，记为 dp[][]。

3）最终状态是 process(arr,0,aim)，也就是 dp[0][aim]的值，位于 dp 表 0 行最后一列。

4）填写初始的位置，根据 process(arr,i,rest)函数的 base case： 

1
2
3
if (i == arr.length) {
    return rest == 0 ? 0 : -1;
}

i=arr.length，就是 dp 表中最后一行 dp[N][…]，这最后一行只有 dp[N][0]是 0，其他位置都是-1。

5） base case 之外的情况都是普遍位置，在 process (arr,i,rest)函数中如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
// 最少张数，初始时为-1，因为还没有找到有效解
int res = -1;
// 依次尝试使用当前面值的（arr[i]）0张，1张，2张...但是总面值不能超过rest
for (int k = 0; k * arr[i] <= rest; k++) {
    // 使用了k张arr[i], 剩下的钱为rest-arr[i]
    // 交给剩下的面值去搞定
    int next = process(arr, i + 1, rest - k * arr[i]);
    if (next != -1) {
        res = res == -1 ? next + k : Math.min(res, next + k);
        // 这一行代码很难理解
    }
}
return res;

process (arr,i,rest)的返回值就是 dp[i][rest]，这个位置依赖哪些位置呢？ 请看下表。

表中右上角的位置就是 dp[i][rest]，根据 process (arr,i,rest)函数可知， dp[i][rest]的值就是以下这些值中最小的一个： dp[i+1][rest-0arr[i]] + 0、 dp[i+1][rest-1arr[i]] + 1、 dp[i+1][rest-2arr[i]] + 2、 …dp[i+1][rest-karr[i]] + k、 ……直到越界。在表中已经标出了这些位置。也就是说， 要想得到dp[i][rest]的值，必须枚举 i+1 行的这些值。

但其实这个枚举过程是可以优化的。请看表中用星号标出的位置，即 dp[i][rest-arr[i]]这个位置。如果在求 dp[i][rest]之前， dp[i][rest-arr[i]]已经求过了。那么我们看看 dp[i][rest-arr[i]]是怎么求出来的，同样， 根据process (arr,i,rest)函数可知， dp[i][rest-arr[i]]的值就是以下这些值中最小的一个： dp[i+1][rest-arr[i]] + 0、 dp[i][rest-2arr[i]] + 1、 … dp[i+1][rest-karr[i]] + k - 1、 ……直到越界。读者请对比一下 dp[i][rest]和 dp[i][rest-arr[i]]各自依赖的位置就可以得到， dp[i][rest] =min{ dp[i][rest-arr[i]] + 1, dp[i+1][rest] }。也就是说， 求 dp[i][rest]只依赖下面的一个位置（dp[i+1][rest]）和左边的一个位置（dp[i][rest-arr[i]] + 1）即可。

现在 dp 表中最后一排的值已经有了，既然剩下的位置都只依赖下面和左边的位置，那么只要从左往右求出倒数第二排、从左往右求出倒数第三排……从左往右求出第一排即可。

6）最后返回 dp[0][aim]位置的值就是答案。

具体过程请看如下的 minCoins2 方法:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public int minCoins2(int[] arr, int aim) {
    if (arr == null || arr.length == 0 || aim < 0) {
        return -1;
    }
    int N = arr.length;
    int[][] dp = new int[N+1][aim+1];
    // 设置最后一排的值，除dp[N][0]为0外，其它都是-1
    for (int col = 1; col <= aim; col++) {
        dp[N][col] = -1;
    }
    for (int i = N - 1; i >= 0; i--) {
        // 从底向上计算每一行
        for (int res = 0; rest <= aim; rest++) {
            // 每一行都从左到右
            dp[i][rest] = -1;  // 初始时设置dp[i][rest]的值无效
            if (dp[i+1][rest] != -1) {
                // 下面的值如果有效
                dp[i][rest] = dp[i+1][rest]  // 先设置成下面的值
            }
            // 如果左边的位置不越界且有效
            if (rest - arr[i] >= 0 && dp[i][rest-arr[i]] != -1) {
                if (dp[i][rest] == -1) {
                    // 如果之前下面的值无效
                    dp[i][rest] = dp[i][rest - arr[i]] + 1;
                } else {
                    // 说明下面和左边的值都是有效的，取最小的
                    dp[i][rest] = Math.min(dp[i][rest], dp[i][rest-arr[i]] + 1);
                }
            }
        }
    }
    return dp[0][aim];
}

minCoins2 方法就是填一张 N×aim 的表，而且因为省掉了枚举过程，所以每个位置的值都在 O(1)的时间内得到， 该方法时间复杂度为 O(N×aim)。原问题还可以在动态规划基础上做空间压缩。空间压缩的原理请读者参考本书“矩阵的最小路径和”问题， 本书这里就不做重复描述。

题目四：机器人达到指定位置的方法数

【题目】

假设有排成一行的 N 个位置，记为 1~N， N 一定大于或等于 2。开始时机器人在其中的 M位置上（M 一定是 1～N 中的一个），机器人可以往左走或者往右走，如果机器人来到 1 位置，那么下一步只能往右来到 2 位置；如果机器人来到 N 位置，那么下一步只能往左来到 N-1 位置。规定机器人必须走 K 步，最终能来到 P 位置（P 也一定是 1～N 中的一个）的方法有多少种。给定四个参数 N、 M、 K、 P，返回方法数。

【举例】

N=5,M=2,K=3,P=3

上面的参数代表所有位置为 1 2 3 4 5。机器人最开始在 2 位置上，必须经过 3 步， 最后到达 3 位置。走的方法只有如下 3 种：
1）从 2 到 1，从 1 到 2，从 2 到 3

2）从 2 到 3，从 3 到 2，从 2 到 3

3）从 2 到 3，从 3 到 4，从 4 到 3

所以返回方法数 3。

N=3,M=1,K=3,P=3

上面的参数代表所有位置为 1 2 3。机器人最开始在 1 位置上，必须经过 3 步， 最后到达 3 位置。怎么走也不可能，所以返回方法数 0。

【难度】

【解答】

这道题不算难，但是在全书的地位极高，因为通过这道题总结了用暴力递归解决的方法如何优化成动态规划的套路。这个套路可以解决大量的类似问题。首先介绍本题暴力递归方法，想想怎么去尝试走所有的路。如果当前来到 cur 位置，还剩 rest 步要走，那么下一步该怎么走呢？如果当前 cur=1， 下一步只能走到 2，后续还剩下 rest-1 步；如果当前 cur=N，下一步只能走到 N-1，后续还剩 rest-1 步；如果 cur 是 1~N 中间的位置，下一步可以走到 cur-1 或者 cur+1，后续还剩 rest-1 步。每一种能走的可能都尝试一遍，每一次尝试怎么算结束？所有步数都走完了，尝试就可以结束了。如果走完了所有的步数，最后的位置停在了 P，说明这次尝试有效，即找到了 1 种；如果最后的位置没有停在 P，说明这次尝试无效，即找到了 0 种。尝试的递归过程请看如下 walk 方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// N : 位置为 1 ~ N，固定参数
// cur : 当前在 cur 位置，可变参数
// rest : 还剩 res 步没有走，可变参数
// P : 最终目标位置是 P，固定参数
// 只能在 1~N 这些位置上移动，当前在 cur 位置，走完 rest 步之后，停在 P 位置的方法数作为返回值返回
public int walk(int N, int cur, int rest, int P) {
    if (rest == 0) {
        return cur == P ? 1 : 0;
    }
    if (cur == 1) {
        return walk(N, 2, rest - 1, P);
    }
    if (cur == N) {
        return walk(N, N - 1, rest - 1, P);
    }
    return walk(N, cur - 1, rest - 1, P) + walk(N, cur + 1, rest - 1, P);
}

尝试是从哪里开始的？是从题目给定的 N、 M、 K、 P 开始的，主方法见如下 ways1 方法。 

1
2
3
4
5
6
7
public int ways1(int N, int M, int K, int P) {
    // 参数无效直接返回 0
    if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
        return 0;
    }
    return walk(N, M, K, P);
}

解决一个问题，如果没有想到显而易见的求解策略（比如数学公式、贪心策略等，都是显而易见的求解策略）， 那么就想如何通过尝试的方式找到答案，一旦写出了好的尝试函数，后面的优化过程全是固定套路。下面介绍本题如何从暴力递归优化成动态规划的解法。暴力递归优化成动态规划时， 首先根据 walk 函数的含义结合题意，分析整个递归过程是不是无后效性的。代码面试中出现的需要利用尝试解法解决的问题，绝大多数都是无后效性的，有后效性的递归过程在面试中出现的情况极其罕见，这是一个真实情况，本书不再详述。但是分析一个递归过程是不是无后效性的，依然非常重要，可以帮我们确定这个暴力递归能不能改成动态规划。所谓无后效性， 是指一个递归状态的返回值与怎么到达这个状态的路径无关。

比如本题， walk 函数有两个固定参数 N 和 P，任何时候都不变，说明 N 和 P 与具体的递归状态无关，忽略它们。只需要关注可变参数 cur 和 rest。 walk(cur, rest)表示的含义是，当前来到cur 位置，还剩 rest 步，有效方法有多少种。比如 cur=5， rest=7，代表当前来到 5 位置，还剩 7 步，有效方法有多少种。 下图画出了如果想求出 walk(5, 7)，状态的依赖关系。

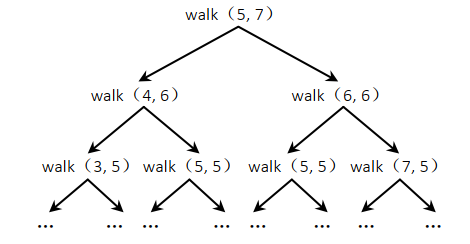
上图中， walk(5,5)状态出现了两次，含义是当前来到 5 位置，还剩 5 步，有效方法有多少种。那么最终的返回值与怎么到达这个状态的路径有关系吗？没有。不管是从 walk(4,6) 来到 walk(5,5)，还是从 walk(6,6)来到 walk(5,5)，只要是“当前来到 5 位置，还剩 5 步”这个问题，返回值都是不变的。所以这是一个无后效性问题。接下来的分析与原始题意已经没有关系了，某个无后效性的递归过程（尝试过程）一旦确定，怎么优化成动态规划是有固定套路的。请读者好好阅读下面的文字，理解这个套路。这个套路可以解决面试中绝大多数尝试性算法的优化。

套路大体步骤如下：

前提：你的尝试过程是无后效性的。

1）找到什么可变参数可以代表一个递归状态，也就是哪些参数一旦确定，返回值就确定了。
2）把可变参数的所有组合映射成一张表，有 1 个可变参数就是一维表， 2 个可变参数就是二维表……
3）最终答案要的是表中的哪个位置，在表中标出。
4）根据递归过程的 base case，把这张表最简单、不需要依赖其他位置的那些位置填好值。
5）根据递归过程非 base case 的部分，也就是分析表中的普遍位置需要怎么计算得到，那么这张表的填写顺序也就确定了。
6）填好表，返回最终答案在表中位置的值。

下面以本题为例来使用这个套路。假设想求， N=7， M=4， K=9， P=5 的答案。

前提： walk 方法是无后效性的，满足前提。

1） walk 函数中，可变参数 cur 和 rest 一旦确定，返回值就确定了。

2） 如果可变参数 cur 和 rest 组合的所有情况组成一张表，这张表一定可以装下所有的返回值。 cur 变量的含义是当前来到的位置，例子给的 N 代表一共有 1～7 这些位置，所以 cur 一定不会在 1～7 的范围之外； rest 变量的含义是还剩多少步，例子给的 K 代表最开始走的时候的剩余步数，走的过程中剩余步数一定是减小的，所以 rest 一定不会在 0～9 范围之外。那么 cur 和rest 组合的所有情况如下图所示，这是一张二维表。

上图中，列对应的是 cur（范围为 1～7），行对应的是 rest（范围为 0～9），其实谁做行对应，谁做列对应是无所谓的，只要能枚举所有的组合即可。任何一个状态 walk(cur,rest)都一定可以放在这张表中。这张表是一个二维数组，记为dp[][]，那么 walk(cur,rest)的返回值就是dp[rest][cur]。

3） N=7， M=4， K=9， P=5 的最终答案，就是 dp[9][4]位置的值，在上图中已经用星号标出。
那么如何求出这个值呢？

4）递归过程的 base case 是指问题的规模小到什么程度，就不需要再划分子问题，答案就
可以直接得到了。 walk 函数中的 base case 如下： 

1
2
3
if (rest == 0) {
    return cur == P ? 1 : 0;
}

当 rest=0 时，如果 cur=P，返回 1；否则返回 0。本题中 P=5。 所以可以把表的第一行填好，表中第一行的所有状态都是最简单且不需要依赖其他位置的。

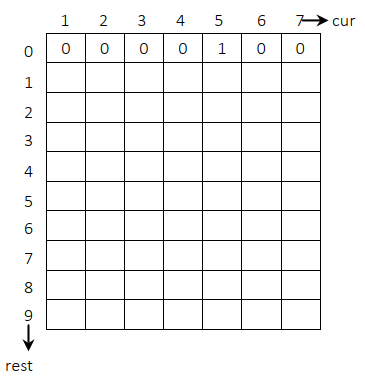
5） base case 之外的情况都是普遍位置，在 walk 函数中如下： 

1
2
3
4
5
6
7
if (cur == 1) {
    return walk(N, 2, rest - 1, P);
}
if (cur == N) {
    return walk(N, N - 1, rest - 1, P);
}
return walk(N, cur + 1, rest - 1, P) + walk(N, cur - 1, rest - 1, P);

如果 cur 在 1 位置，最终返回值 dp[rest][cur]=dp[rest-1][2]（下图中 A 点依赖 B 点）；如果 cur 在 N 位置，最终返回值dp[rest][cur]=dp[rest-1][N-1]（下图中 C 点依赖 D 点）；如果 cur 在中间位置， dp[rest][cur]=dp[rest-1][cur-1]+dp[rest-1][cur+1]（下图中 E 点依赖 F 点和 G 点）。

这说明每一行的值都只依赖上一行的值，那么如果有了第一行的值，就可以推出整张表。整张表的值如下图所示。

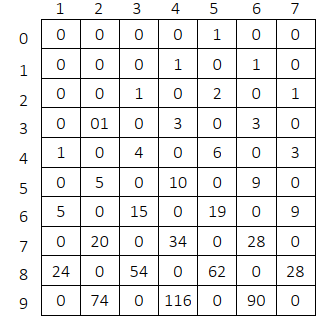
6）返回 dp[9][4]的值，答案是 116。

这个套路是非常好用的，一旦尝试函数确定了，优化是不需要再考虑原始题意的，只需要考虑状态依赖关系，填好表即可。如果你已经累积了大量动态规划的技巧并且已经运用自如，这个套路对你来讲可能并不重要。但情况往往是绝大多数人对动态规划理解不深刻，经验不丰富， 本书提供的套路解法会帮你尽快建立起对动态规划题目的感觉。从尝试出发，一切优化水到渠成。本书还有很多题目涉及这个套路，还会帮读者强化这个内容。但是有后效性的尝试过程，本套路是失效的，这类题目在面试中出现的概率极低。

本题动态规划的解法就是把规模为 N×K 的表填好，填写每一个位置的值都是 O(1)的时间复杂度，所以总的时间复杂度为O(N×K)，请看如下的 ways2 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int ways2(int N, int M, int K, int P) {
    // 参数无效直接返回
    if (N < 2, || K < 1 || M < 1 || M > N || P < 1 || P > N) {
        return 0;
    }
    int[][] dp = new int[K+1][N+1];
    dp[0][P] = 1;
    for (int i = 1; i <= K; i++) {
        for (int j = 1; j <= N; j++) {
            if (j == 1) {
                dp[i][j] = dp[i-1][2];
            } else if (j == N) {
                dp[i][j] = dp[i-1][N-1];
            } else {
                dp[i][j] = dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1];
            }
        }
    }
    return dp[K][M];
}

本题动态规划+空间压缩的解法，请看如下的 ways3 方法。空间压缩技巧在本章“最短路径和”问题的解答中已经详细介绍过了，这里不再详述。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int ways3(int N, int M, int K, int P) {
    if (N < 2 || K < 1 || M < 1 || M > N || P < 1 || P > N) {
        return 0;
    }
    int[] dp = new int[N+1];
    dp[P] = 1;
    for (int i = 1; i <= K; i++) {
        int leftUp = dp[1];  // 左上角的值
        for (int j = 1; j <= N; j++) {
            int tmp dp[j];
            if (j == 1) {
                dp[j] = dp[j+1];
            } else if (j == N) {
                dp[j] = leftUp;
            } else {
                dp[j] = leftUp + dp[j+1];
            }
            leftUp = tmp;
        }
    }
    return dp[M];
}

题目五：换钱方法数

【题目】

给定数组 arr， arr 中所有的值都为正数且不重复。每个值代表一种面值的货币，每种面值的货币可以使用任意张， 再给定一个整数 aim， 代表要找的钱数， 求换钱有多少种方法。

【举例】

arr=[5,10,25,1]， aim=0。
组成 0 元的方法有 1 种，就是所有面值的货币都不用。所以返回 1。

arr=[5,10,25,1]， aim=15。
组成 15 元的方法有 6 种，分别为 3 张 5 元、 1 张 10 元+1 张 5 元、 1 张 10 元+5 张 1 元、 10 张 1 元+1 张 5 元、 2 张 5 元+5 张 1 元和 15 张 1 元。所以返回 6。

arr=[3,5]， aim=2。
任何方法都无法组成 2 元。所以返回 0 。

【难度】

【解答】

本书将由浅入深地给出所有的解法，最后解释最优解。这道题的经典之处在于它可以体现暴力递归、记忆搜索和动态规划之间的关系，并可以在动态规划的基础上进行再一次优化。 请读者把本书“机器人达到指定位置方法数”问题所提到的套路联系起来。

首先介绍暴力递归的方法。如果 arr=[5,10,25,1]， aim=1000，分析过程如下：

1． 用 0 张 5 元的货币，让[10,25,1]组成剩下的 1000，最终方法数记为 res1。
2． 用 1 张 5 元的货币，让[10,25,1]组成剩下的 995，最终方法数记为 res2。
3． 用 2 张 5 元的货币，让[10,25,1]组成剩下的 990，最终方法数记为 res3。
……
201． 用 200 张 5 元的货币，让[10,25,1]组成剩下的 0，最终方法数记为 res201。

那么 res1+res2+… +res201 的值就是总的方法数。根据如上的分析过程定义递归函数process1(arr,index,aim)，它的含义是如果用 arr[index..N-1]这些面值的钱组成 aim，返回总的方法数。具体实现参见如下代码中的 coins1 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public int coins1(int[] arr, int aim) {
    if (arr == null || arr.length == 0 || aim < 0) {
        return 0;
    }
    return process1(arr, 0, aim);
}
public int process1(int[] arr, int index, int aim) {
    int res = 0;
    if (index == arr.length) {
        res = aim == 0 ? 1 : 0;
    } else {
        for (int i = 0; arr[i] * i <= aim; i++) {
            res += process1(arr, index + 1, aim - arr[i] * i);
        }
    }
    return res;
}

接下来介绍基于暴力递归初步优化的方法，也就是记忆搜索的方法。暴力递归之所以暴力，是因为存在大量的重复计算。比如上面的例子，当已经使用 0 张 5 元+1 张 10 元的情况下，后续应该求[25,1]组成剩下的 990 的方法总数。当已经使用 2 张 5 元+0 张 10 元的情况下，后续还是求[25,1]组成剩下的 990 的方法总数。两种情况下都需要求process1(arr,2,990)。类似这样的重复计算在暴力递归的过程中大量发生，所以暴力递归方法的时间复杂度非常高， 并且与 arr 中钱的面值有关，最差情况下为 $O(aim^{N})$。

记忆化搜索的优化方式。 process1(arr,index,aim)中 arr 是始终不变的，变化的只有 index 和aim，所以可以用p(index,aim)表示一个递归过程。重复计算之所以大量发生，是因为每一个递归过程的结果都没记下来，所以下次还要重复去求。 我们可以事先准备好一个 map，每计算完一个递归过程，都将结果记录到 map 中。当下次进行同样的递归过程之前，先在map 中查询这个递归过程是否已经计算过，如果已经计算过，就把值拿出来直接用，如果没计算过，需要再进入递归过程。具体请参看如下代码中的 coins2 方法，它和 coins1 方法的区别就是准备好全局变量 map，记录已经计算过的递归过程的结果，防止下次重复计算。因为本题的递归过程可由两个变量表示，所以 map 是一张二维表。 map[i][j]表示递归过程 p(i,j)的返回值。另外有一些特殊值， map[i][j]=0 表示递归过程 p(i,j)从来没有计算过。 map[i][j]=-1 表示递归过程 p(i,j)计算过，但返回值是 0。如果 map[i][j]的值既不等于 0， 也不等于-1，记为 a，则表示递归过程 p(i,j)的返回值为 a。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public int coins2(int[] arr, int aim) {
    if (arr == null || arr.length == 0 || aim < 0) {
        return 0;
    }
    int[][] map = new int[arr.length + 1][aim + 1];
    return process2(arr, 0, aim, map);
}
public int process2(int[] arr, int index, int aim, int[][] map) {
    int res = 0;
    if (index == arr.length) {
        res = aim == 0 ? 1 : 0;
    } else {
        int mapValue = 0;
        for (int i = 0; arr[index] * i <= aiml i++) {
            mapValue = map[index + 1][aim - arr[index] * i];
            if (mapValue != 0) {
                res += mapValue == -1 ? 0 : mapValue;
            } else {
                res += process2(arr, index + 1, aim - arr[index] * i, map);
            }
        }
    }
    map[index][aim] = res == 0 ? -1 : res;
    return res;
}

记忆化搜索的方法是针对暴力递归最初级的优化技巧，分析递归函数的状态可以由哪些变量表示，做出相应维度和大小的 map 即可。记忆化搜索方法的时间复杂度为 $O(N×aim^2)$，我们在解释完下面的方法后，再来具体解释为什么是这个时间复杂度。

动态规划方法: 其实就是本书“机器人达到指定位置方法数”问题所提到的套路。 生成行数为 N、 列数为 aim+1 的矩阵 dp， dp[i][j]的含义是在使用 arr[0..i]货币的情况下，组成钱数 j 有多少种方法。 dp[i][j]的值求法如下：

1．对于矩阵 dp 第一列的值 dp[..][0]，表示组成钱数为 0 的方法数，很明显是 1 种，也就是不使用任何货币。所以 dp 第一列的值统一设置为 1。

2．对于矩阵 dp 第一行的值 dp[0][..]，表示只能使用 arr[0]这一种货币的情况下，组成钱的方法数，比如， arr[0]=5 时，能组成的钱数只有 0， 5， 10， 15，…。所以， 令 dp[0][k*arr[0]]=1（0≤k×arr[0]≤aim， k 为非负整数）。

3．除第一行和第一列的其他位置，记为位置(i,j)。 dp[i][j]的值是以下几个值的累加。

  • 完全不用 arr[i]货币，只使用 arr[0..i-1]货币时，方法数为 dp[i-1][j]。
  • 用 1 张 arr[i]货币，剩下的钱用 arr[0..i-1]货币组成时，方法数为 dp[i-1][j-arr[i]]。
  • 用 2 张 arr[i]货币，剩下的钱用 arr[0..i-1]货币组成时， 方法数为 dp[i-1][j-2arr[i]]。
    ……
  • 用 k 张 arr[i]货币，剩下的钱用 arr[0..i-1]货币组成时，方法数为 dp[i-1][j-k*arr[i]]。j-k*arr[i]>=0， k 为非负整数。

4．最终 dp[N-1][aim]的值就是最终结果。

具体过程请参看如下代码中的 coins3 方法:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int coins3(int[] arr, int aim) {
    if (arr == null || arr.length == 0 || aim < 0) {
        return 0;
    }
    int[][] dp = new int[arr.length][aim + 1];
    for (int i = 0; i < arr.length; i++) {
        dp[i][0] = 1;
    }
    for (int j = 1; arr[0] * j <= aim; j++) {
        dp[0][arr[0] * j] = 1;
    }
    int num = 0;
    for (int i = 1; i < arr.length; i++) {
        for (int j = 1; j <= aim; j++) {
            num = 0;
            for (int k = 0; j - arr[i] * k >= 0; k++) {
                num += dp[i - 1][j - arr[i] * k];
            }
            dp[i][j] = num;
        }
    }
    return dp[arr.length - 1][aim];
}

在最差的情况下， 对位置(i,j)来说，求解 dp[i][j]的计算过程需要枚举 dp[i-1][0..j]上的所有值，dp 一共有 N×aim 个位置，所以总体的时间复杂度为 O(N×aim2)。

下面解释之前记忆化搜索方法的时间复杂度为什么也是 $O(N×aim^2)$，因为记忆化搜索方法在本质上等价于动态规划方法。记忆化搜索的方法说白了就是不关心到达某一个递归过程的路径，只是单纯地对计算过的递归过程进行记录，避免重复的递归过程，而动态规划的方法则是规定好每一个递归过程的计算顺序，依次进行计算，后计算的过程严格依赖前面计算过的过程。两者都是空间换时间的方法，也都有枚举的过程，区别就在于动态规划规定计算顺序， 而记忆搜索不用规定。所以记忆化搜索方法的时间复杂度也是 $O(N×aim^2)$。两者各有优缺点，如果将暴力递归过程简单地优化成记忆搜索的方法，递归函数依然在使用，这在工程上的开销较大。而动态规划方法严格规定了计算顺序，可以将递归计算变成顺序计算，这是动态规划方法具有的优势。其实记忆搜索的方法也有优势，本题就很好地体现了。比如， arr=[20000,10000,1000]，aim=2000000000。如果是动态规划的计算方法，要严格计算 3×2000000000 个位置。而对于记忆搜索来说，因为面值最小的钱为 1000，所以百位为（19）、 十位为（19） 或各位为（1~9）的钱数是不可能出现的，当然也就没必要计算。通过本例可以知道，记忆化搜索是对必须要计算的递归过程才去计算并记录的。

接下来介绍时间复杂度为 $O(N×aim)$的动态规划方法。我们来看上一个动态规划方法中，求dp[i][j]值时的步骤 3，这也是最关键的枚举过程：除第一行和第一列的其他位置，记为位置(i,j)。dp[i][j]的值是以下几个值的累加。

  • 完全不用 arr[i]货币，只使用 arr[0..i-1]货币时，方法数为 dp[i-1][j]。
  • 用 1 张 arr[i]货币，剩下的钱用 arr[0..i-1]货币组成时，方法数为 dp[i-1][j-arr[i]]。
  • 用 2 张 arr[i]货币，剩下的钱用 arr[0..i-1]货币组成时，方法数为 dp[i-1][j-2*arr[i]]。
    ……
  • 用 k 张 arr[i]货币，剩下的钱用 arr[0..i-1]货币组成时，方法数为 dp[i-1][j-k*arr[i]]。j-k*arr[i]>=0， k 为非负整数。

步骤 3 中， 第 1 种情况的方法数为 dp[i-1][j]，而第 2 种情况一直到第 k 种情况的方法数累加值其实就是 dp[i][j-arr[i]]的值。所以步骤 3 可以简化为 dp[i][j]=dp[i-1][j]+dp[i][j-arr[i]]。一下省去了枚举的过程，时间复杂度也减小至 $O(N×aim)$，具体请参看如下代码中的 coins4 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int coins4(int[] arr, int aim) {
    if (arr == null || arr.length == 0 || aim < 0) {
        return 0;
    }
    int[][] dp = new int [arr.length][aim + 1];
    for (int i = 0; i < arr.length; i++) {
        dp[i][0] = 1;
    }
    for (int j = 1; arr[0] * j <= aim; j++) {
        dp[0][arr[0] * j] = 1;
    }
    for (int i = 1; i < arr.length; i++) {
        for (int j = 1; j <= aim; j++) {
            dp[i][j] = dp[i - 1][j];
            dp[i][j] += j - arr[j] >= 0 ? dp[i][j - arr[i]] : 0;
        }
    }
    return dp[arr.length - 1][aim];
}

时间复杂度为 O(N×aim)的动态规划方法再结合空间压缩的技巧。空间压缩的原理请读者参考“矩阵的最小路径和”问题，这里不再详述。请参看如下代码中的 coins5 方法:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int coins5(int[] arr, int aim) {
    if (arr == null || arr.length == 0 || aim < 0) {
        return 0;
    }
    int[] dp = new int[aim + 1];
    for (int j = 0; arr[0] * j <= aim; j++) {
        dp[arr[0] * j] = 1;
    }
    for (int i = 1; i < arr.length; i++) {
        for (int j = 1; j <= aim; j++) {
            dp[j] += j - arr[i] >= 0 ? dp[j-arr[i]] : 0;
        }
    }
    return dp[aim];
}

至此， 我们得到了最优解，是时间复杂度为 O(N×aim)、 额外空间复杂度 O(aim)的方法。

【扩展】

通过本题目的优化过程，可以梳理出暴力递归通用的优化过程。对于在面试中遇到的具体题目，面试者一旦想到暴力递归的过程，其实之后的优化过程是水到渠成的。首先看写出来的暴力递归函数，找出有哪些参数是不发生变化的，忽略这些变量。只看那些变化并且可以表示递归过程的参数，找出这些参数之后，记忆搜索的方法其实可以很轻易地写出来，因为只是简单的修改，计算完就记录到 map 中， 并在下次直接拿来使用，没计算过则依然进行递归计算。接下来观察记忆搜索过程中使用的 map 结构，看看该结构某一个具体位置的值是通过哪些位置的值求出的，被依赖的位置先求，就能改出动态规划的方法，也就是本书“机器人达到指定位置方法数”问题提到的套路。改出的动态规划方法中，如果有枚举的过程，看看枚举过程是否可以继续优化，常规的方法既有本题所实现的通过表达式来化简枚举状态的方式，也有本书的“丢棋子问题”、“画匠问题”和“邮局选址问题”所涉及的四边形不等式的相关内容，有兴趣的读者可以进一步学习。

题目六：打气球的最大分数

【题目】

给定一个数组 arr，代表一排有分数的气球。每打爆一个气球都能获得分数，假设打爆气球的分数为 X，获得分数的规则如下：

1）如果被打爆气球的左边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为L；如果被打爆气球的右边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为 R。获得分数为 L×X×R。

2）如果被打爆气球的左边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数L；如果被打爆气球的右边所有气球都已经被打爆。获得分数为 L×X。

3）如果被打爆气球的左边所有的气球都已经被打爆；如果被打爆气球的右边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为 R；如果被打爆气球的右边所有气球都已经被打爆。获得分数为 X×R。

4）如果被打爆气球的左边和右边所有的气球都已经被打爆。获得分数为 X。目标是打爆所有气球，获得每次打爆的分数。通过选择打爆气球的顺序，可以得到不同的总分，请返回能获得的最大分数。

【相关题目】

LeetCode 312.戳气球

【难度】

【要求】

如果 arr 长度为 N，时间复杂度$ O(N^3) $。

【解答】

这道题我们使用暴力递归优化成动态规划的套路，不熟悉套路的读者请先阅读本书“机器人达到指定位置方法数”问题的解答。本题先实现尝试出所有可能打爆方法的暴力递归过程。只有尝试方法是最重要的，而且没有任何固定套路可以总结如何去尝试。

假设要打爆 arr[L..R]这个范围上所有的气球，并且假设 arr[L-1]和 arr[R+1]的气球都没有被打爆，尝试的过程为 process 函数，最后获得的最大分数为 process(L,R)。依次尝试，如果每个气球最后被打爆，具体为：

如果 arr[L]是最后被打爆的，也就是先把 arr[L+1..R]范围上的气球都打完之后， 再打爆 arr[L]。先把 arr[L+1..R]范围上的气球都打完能够获得的最大分数为 process(L+1,R)。因为此时 arr[L+1..R]的气球都打完了，所以 arr[L]的左边为 arr[L-1]，右边为 arr[R+1]，最后打爆 arr[L]获得的分数为arr[L-1] * arr[L] * arr[R+1]， 总分为 arr[L-1] * arr[L] * arr[R+1] + process(L+1,R)。

如果 arr[L+1]是最后被打爆的，也就是先把 arr[L..L]和 arr[L+2..R]范围上的气球都打完之后，再打爆 arr[L+1]。把 arr[L..L]范围上的气球都打完能够获得的最大分数为 process(L,L)，把 arr[L+2..R]范围上的气球都打完能够获得的最大分数为 process(L+2,R)。因为此时 arr[L..L]和 arr[L+2..R]的气球都打完了，所以 arr[L+1]的左边为 arr[L-1]，右边为 arr[R+1]，最后打爆 arr[L]获得的分数为arr[L-1] * arr[L+1] * arr[R+1]， 总分为 process(L,L) + process (L+2,R)+arr[L-1] * arr[L] * arr[R+1]。

……

如果 arr[R]是最后被打爆的，也就是先把 arr[L..R-1]范围上的气球都打完之后， 再打爆 arr[R]。先把 arr[L..R-1]范围上的气球都打完能够获得的最大分数为 process(L,R-1)。因为此时 arr[L..R-1]的气球都打完了，所以 arr[R]的左边为 arr[L-1]，右边为 arr[R+1]，最后打爆 arr[R]获得的分数为arr[L-1] * arr[R] * arr[R+1]， 总分为 process(L,R-1) + arr[L-1] * arr[R] * arr[R+1]。

以上所有的尝试方案中， 哪个方案的总分最大，哪个就是 process(L,R)的返回值。以上解释的所有尝试过程请看如下的 process 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 打爆arr[L..R]范围的所有气球，返回最大的分数
// 假设arr[L-1] 和arr[R+1]一定没有被打爆
public int process(int[] arr, int L, int R) {
    if (L == R) {
        return arr[L - 1] * arr[L] * arr[L + 1];
    }
    // 最后打爆arr[L]的方案与最后打爆arr[R]的方案，先比较一下
    int max = Math.max(arr[L - 1] * arr[L] * arr[R + 1] + process(arr, L + 1, R), arr[L - 1] * arr[R] * arr[R + 1] + process(arr, L, R - 1));
    // 尝试中间的位置汽车被打爆的每一种方案
    // 比较每种方案，取结果最大值
    for (int i = L + 1; i < R; i++) {
        max = Math.max(max, process(arr, L, i - 1) + process(arr, i + 1, R) + arr[L - 1] * arr[i] * arr[R + 1]);
    }
    return max;
}

如果把 arr 的开头和结尾补上 1，然后打爆除两头的 1 还剩下的位置，就是答案。比如arr={3,2,5}，先生成一个辅助数组 help={1,3,2,5,1}，然后打爆 help[1..3]范围上（即[3,2,5]） 的所有气球即可，这么做可以避免判断越界所带来的编程烦恼。主方法请看如下的 maxCoins1 方法，尝试的解法已经完全实现了。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int maxCoinsl(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    if (arr.length == 1) {
        return arr[0];
    }
    int N = arr.length;
    int[] help = new int [N + 2];
    help[0] = 1;
    help[N + 1] = 1;
    for (int i = 0; i < N; i++) {
        help[i + 1] = arr[i];
    }
    return process(help, 1, N);
}

这种方法在解 Leetcode 312题 戳气球 的时候超出时间限制，掌握动态规划的方法很重要。

暴力递归改动态规划。假设 arr={4,2,3,5,1,6}，生成的 help={1,4,2,3,5,1,6,1}，求的是打爆help[1..6]上的所有气球获得的最大分数。利用优化套路过程如下。

前提：尝试过程是无后效性的。 process(L,R)解决的问题就是打爆 help[L..R]上所有的气球获得的最大分数，不管如何到达的 process(L,R)，返回值一定是固定的。

1）可变参数 L 和 R 一旦确定，返回值就确定了。

2）如果可变参数 L 和 R 组合的所有情况组成一张表，这张表一定可以装下所有的返回值。L 变量的含义是 help 中的位置，所以 L 一定不会在 1～6 的范围之外； R 变量的含义是 help 中的位置，所以 L 一定不会在 1～6 范围之外。那么 L 和 R 组合的所有情况如图 4-6 所示，这是一个正方形矩阵。

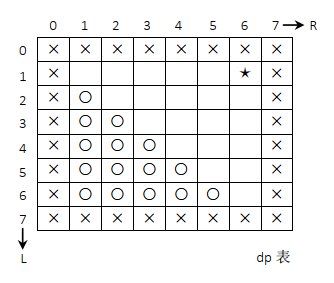
在上图中， 行对应 L， 列对应 R，枚举了 L 和 R 所有的组合即可，其中第 0 行、第 7 行、第 0 列和第 7 列是永远不会用到的，这些位置在图中已经用叉号标出。因为 process(L,R)表达的含义是在 help[L..R]这个范围上做尝试，所以 L 不可能大于 R。 也就是说， 这张表中不含对角线的下半区（L>R） 是永远不会用到的，这些位置在图中已经用圆圈标出。任何一个状态 process(L,R)都一定可以放在剩下的位置中，这张表记为 dp[][]。

3）我们要的最终状态是 process(1,6)，也就是 dp[1][6]的值，在表中已经用星号标出。如何求出这个值呢？

4）根据 process(L,R)函数的 base case， 填写初始的位置：

1
2
3
if (L == R) {
    return help[L - 1] * help[L] * help[R + 1];
}

L==R 时，就是下图中的对角线位置，如果对角线位置是 dp[i][i]，那么 dp[i][i]=help[i - 1] * help[i] * help[i + 1]。填写之后如下图所示。

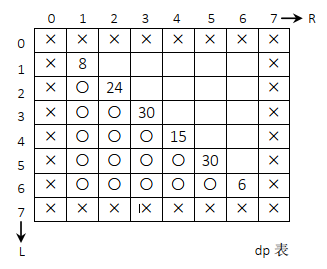
5）base case 之外的情况都是普遍位置，在 process(L,R)函数中如下： 

1
2
3
4
5
6
int max = Math.max(arr[L - 1] * arr[L] * arr[R + 1] + process(arr, L + 1, R), arr[L - 1] * arr[R] * arr[R + 1] + process(arr, L, R - 1));
// 尝试中间的位置汽车被打爆的每一种方案
// 比较每种方案，取结果最大值
for (int i = L + 1; i < R; i++) {
    max = Math.max(max, process(arr, L, i - 1) + process(arr, i + 1, R) + arr[L - 1] * arr[i] * arr[R + 1]);
}

如果用看代码的方式分析状态依赖不直观，可以用分析 dp 表的方式。比如 dp[1][6]这个位置（星号），依赖哪些位置呢？根据 process(L,R)的代码，分析出 process(1,6)依赖的位置有：

1） process(2,6)，最后打爆 help[1]时的依赖， 下图中的 A。

2） process(1,5)，最后打爆 help[6]时的依赖， 下图中的 B。

3） process(1,1)，最后打爆 help[2]时的依赖， 下图中的 C。

4） process(3,6)，最后打爆 help[2]时的依赖， 下图中的 D。

5） process(1,2)，最后打爆 help[3]时的依赖， 下图中的 E。

6） process(4,6)，最后打爆 help[3]时的依赖， 下图中的 F。

7） process(1,3)，最后打爆 help[4]时的依赖， 下图中的 G。

8） process(5,6)，最后打爆 help[4]时的依赖， 下图中的 H。

9） process(1,4)，最后打爆 help[5]时的依赖， 下图中的 I。

10） process(6,6)，最后打爆 help[5]时的依赖， 下图中的 J。

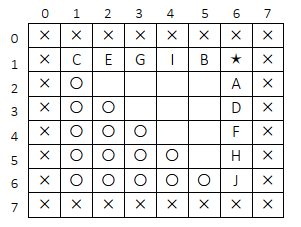
这说明 dp[L][R]值都只依赖同一行左边和同一列下边的有效位置，已经标为无效的位置依然不需要。所以，除去对角线， 剩下的位置应该怎么填呢？先填最下面的行，从左往右进行填写；填好一行之后，再从左往右填写上一行。最终填写到有效部分的最上面一行，最右的有效位置就是答案。按照这种顺序求解任何一个位置的值时，这个位置左边和下面的位置一定已经被填写过了。

6）返回 dp[1][6]的值就是答案。

本题动态规划的解法就是填写一个规模 O($N^2$)表的上半区，填写每一个位置的时候，都有一个时间复杂度 O(N)的枚举过程，所以整体的时间复杂度为 O($N^3$)。具体实现请看如下的 maxCoins2方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public int maxCoins2(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    if (arr.length == 1) {
        return arr[0];
    }
    int N = arr.length;
    int[] help = new int[N + 2];
    help[0] = 1;
    help[N + 1] = 1;
    for (int i = 0; i < N; i++) {
        help[i + 1] = arr[i];
    }
    int[][] dp = new int [N + 2][N + 2];
    for (int i = 1; i <= N; i++) {
        dp[i][i] = help[i-1] * help[i] * help[i + 1];
    }
    for (int L = N; L >= 1; L--) {
        for (int R = L + 1; R <= N; R++) {
            // 求解dp[L][R], 表示help[L..R]上打爆所有气球的最大分数
            // 最后打爆help[L]的方案
            int finalL = help[L - 1] * help[L] * help[R + 1] + dp[L + 1][R];
            // 最后打爆help[R]的方案
            int finalR = help[L - 1] * help[R] * help[R + 1] + dp[L][R - 1];
            // 先比较一下最后打爆help[L]和最后打爆help[R]的方案
            dp[L][R] = Math.max(finalL, finalR);
            // 尝试中间位置的气球被最后打爆的每一种方案
            for (int i = L + 1; i < R; i++) {
                dp[L][R] = Math.max(dp[L][R], help[L-1] * help[i] * help[R + 1] + dp[L][i - 1] + dp[i + 1][R]);
            }
        }
    }
    retrun dp[1][N];
}

题目七：最长递增子序列

【题目】

给定数组 arr，返回 arr 的最长递增子序列。

【举例】

arr=[2,1,5,3,6,4,8,9,7]，返回的最长递增子序列为[1,3,4,8,9]。

【要求】

如果 arr 长度为 N，请实现时间复杂度为 O(NlogN)的方法。

【难度】

【相关题目】

LeetCode 300.最长递增子序列

【解答】

先介绍时间复杂度为 O(N2)的方法，具体过程如下：

1．生成长度为 N 的数组 dp， dp[i]表示在以 arr[i]这个数结尾的情况下， arr[0..i]中的最大递增子序列长度。

2．对第一个数 arr[0]来说， 令 dp[0]=1，接下来从左到右依次算出以每个位置的数结尾的情况下，最长递增子序列长度。

3．假设计算到位置 i，求以 arr[i]结尾情况下的最长递增子序列长度， 即 dp[i]。如果最长递增子序列以 arr[i]结尾，那么在 arr[0..i-1]中所有比 arr[i]小的数都可以作为倒数第二个数。在这么多倒数第二个数的选择中，以哪个数结尾的最大递增子序列更大，就选哪个数作为倒数第二个数，所以 dp[i]=max{dp[j]+1(0<=j<i， arr[j]<arr[i])}。如果arr[0..i-1]中所有的数都不比 arr[i]小，令dp[i]=1 即可，说明以 arr[i]结尾情况下的最长递增子序列只包含arr[i]。

按照步骤 1~步骤 3 可以计算出 dp 数组，具体过程请参看如下代码中的 getdp1 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
public int[] getdp1(int[] arr) {
    int[] dp = new int[arr.length];
    for (int i = 0; i < arr.length; i++) {
        dp[i] = 1;
        for (int j = 0; j < i; j++) {
            if (arr[i] > arr[j]) {
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
    }
    return dp;
}

接下来解释如何根据求出的 dp 数组得到最长递增子序列。 以题目的例子来说明，arr=[2,1,5,3,6,4,8,9,7]，求出的数组 dp=[1,1,2,2,3,3,4,5,4].

1． 遍历 dp 数组，找到最大值以及位置。在本例中， 最大值为 5，位置为 7， 说明最终的最长递增子序列的长度为 5，并且应该以 arr[7]这个数（arr[7]=9） 结尾。

2． 从 arr 数组的位置 7 开始从右向左遍历。如果对某一个位置 i，既有 arr[i]<arr[7]， 又有dp[i]=dp[7]-1，说明 arr[i]可以作为最长递增子序列的倒数第二个数。在本例中， arr[6]<arr[7]，并且 dp[6]=dp[7]-1，所以 8 应该作为最长递增子序列的倒数第二个数。

3． 从 arr 数组的位置 6 开始继续向左遍历，按照同样的过程找到倒数第三个数。在本例中，位置 5 满足 arr[5]<arr[6]， 并且 dp[5]=dp[6]-1，同时位置 4 也满足。选 arr[5] 或者 arr[4]作为倒数第三个数都可以。

4． 重复这样的过程，直到所有的数都找出来。dp 数组包含每一步决策的信息，其实根据 dp 数组找出最长递增子序列的过程就是从某一个位置开始逆序还原出决策路径的过程。具体过程请参看如下代码中的 generateLIS 方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int[] generateLIS(int[] arr, int[] dp) {
    int len = 0;
    int index = 0;
    for (int i = 0; i < dp.length; i++) {
        if (dp[i] > len) {
            len = dp[i];
            index = i;
        }
    }
    int[] lis = new int[len];
    lis[--len] = arr[index];
    for (int i = index; i >= 0; i--) {
        if (arr[i] < arr[index] && dp[i] == dp[index] - 1) {
            lis[--len] = arr[i];
            index = i;
        }
    }
    return lis;
}

整个过程的主方法参看如下代码中的 lis1 方法。 

1
2
3
4
5
6
7
public int[] lis1(int[] arr) {
    if (arr == null || arr.length == 0) {
        return null;
    }
    int[] dp = getdpl(arr);
    return generateLIS(arr, dp);
}

很明显，计算 dp 数组过程的时间复杂度为 O($N^2$)，根据 dp 数组得到最长递增子序列过程的时间复杂度为 O(N)，所以整个过程的时间复杂度为 O($N^2$)。如果让时间复杂度达到 O($NlogN$)，只要让计算 dp 数组的过程达到时间复杂度 O($NlogN$)即可，之后根据 dp 数组生成最长递增子序列的过程是一样的。

时间复杂度 O($NlogN$)生成 dp 数组的过程是利用二分查找来进行的优化。先生成一个长度为 N 的数组 ends，初始时 ends[0]=arr[0]，其他位置上的值为 0。生成整型变量 right，初始时 right=0。在从左到右遍历 arr 数组的过程中，求解 dp[i]的过程需要使用 ends 数组和 right 变量，所以这里解释一下其含义。遍历的过程中， ends[0..right]为有效区， ends[right+1..N-1]为无效区。对有效区上的位置 b，如果有 ends[b]=c，则表示遍历到目前为止，在所有长度为 b+1 的递增序列中，最小的结尾数是 c。无效区的位置则没有意义。

比如， arr=[2,1,5,3,6,4,8,9,7]，初始时 dp[0]=1， ends[0]=2， right=0。 ends[0..0]为有效区，ends[0]=2 的含义是，在遍历过 arr[0]之后，所有长度为 1 的递增序列中（此时只有[2]），最小的结尾数是 2。之后的遍历继续用这个例子来说明求解过程。

1． 遍历到 arr[1]=1。 ends 有效区=ends[0..0]=[2]，在有效区中找到最左边大于或等于 arr[1]的数。发现是ends[0]，表示以 arr[1]结尾的最长递增序列只有 arr[1]，所以令 dp[1]=1。然后令ends[0]=1，因为遍历到目前为止，在所有长度为 1 的递增序列中，最小的结尾数是 1， 而不再是 2。

2． 遍历到 arr[2]=5。 ends 有效区=ends[0..0]=[1]，在有效区中找到最左边大于或等于 arr[2]的数。发现没有这样的数，表示以 arr[2]结尾的最长递增序列长度=ends 有效区长度+1，所以令 dp[2]=2。 ends 整个有效区都没有比 arr[2]更大的数，说明发现了比 ends 有效区长度更长的递增序列，于是把有效区扩大， ends 有效区=ends[0..1]=[1,5]。

3． 遍历到 arr[3]=3。 ends 有效区=ends[0..1]=[1,5]，在有效区中用二分法找到最左边大于或等于 arr[3]的数。发现是 ends[1]，表示以 arr[3]结尾的最长递增序列长度为 2，所以令 dp[3]=2。然后令 ends[1]=3，因为遍历到目前为止，在所有长度为 2 的递增序列中，最小的结尾数是 3，而不再是 5。

4． 遍历到 arr[4]=6。 ends 有效区=ends[0..1]=[1,3]，在有效区中用二分法找到最左边大于或等于 arr[4]的数。发现没有这样的数，表示以 arr[4]结尾的最长递增序列长度=ends 有效区长度+1，所以令 dp[4]=3。 ends 整个有效区都没有比 arr[4]更大的数，说明发现了比 ends 有效区长度更长的递增序列，于是把有效区扩大， ends 有效区=ends[0..2]=[1,3,6]。

5． 遍历到 arr[5]=4。 ends 有效区=ends[0..2]=[1,3,6]，在有效区中用二分法找到最左边大于或等于 arr[5]的数。发现是 ends[2]，表示以 arr[5]结尾的最长递增序列长度为 3，所以令 dp[5]=3。然后令 ends[2]=4，表示在所有长度为 3 的递增序列中，最小的结尾数变为 4。

6． 遍历到 arr[6]=8。 ends 有效区=ends[0..2]=[1,3,4]，在有效区中用二分法找到最左边大于或等于 arr[6]的数。发现没有这样的数，表示以 arr[6]结尾的最长递增序列长度=ends 有效区长度+1，所以令 dp[6]=4。 ends 整个有效区都没有比 arr[6]更大的数，说明发现了比 ends 有效区长度更长的递增序列，于是把有效区扩大， ends 有效区=ends[0..3]=[1,3,4,8]。

7． 遍历到 arr[7]=9。 ends 有效区=ends[0..3]=[1,3,4,8]，在有效区中用二分法找到最左边大于或等于 arr[7]的数。发现没有这样的数，表示以 arr[7]结尾的最长递增序列长度=ends 有效区长度+1，所以令 dp[7]=5。 ends 整个有效区都没有比 arr[7]更大的数，于是把有效区扩大， ends 有效区=ends[0..5]=[1,3,4,8,9]。

8． 遍历到 arr[8]=7。 ends 有效区=ends[0..5]=[1,3,4,8,9]，在有效区中用二分法找到最左边大于或等于 arr[8]的数。发现是 ends[3]，表示以 arr[8]结尾的最长递增序列长度为 4，所以令 dp[8]=4。然后令 ends[3]=7，表示在所有长度为 4 的递增序列中，最小的结尾数变为 7。

具体过程请参看如下代码中的 getdp2 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public int[] getdp2(int[] arr) {
    int[] dp = new int[arr.length];
    int[] ends = new int[arr.length];
    ends[0] = arr[0];
    dp[0] = 1;
    int right = 0;
    int l = 0;
    int r = 0;
    int m = 0;
    for (int i = 1; i < arr.length; i++) {
        l = 0;
        r = right;
        while (l <= r) {
            m = (l + r) / 2;
            if (arr[i] > ends[m]) {
                l = m + 1;
            } else {
                r = m - 1;
            }
        }
        right = Math.max(right, l);
        ends[l] = arr[i];
        dp[i] = l + 1;
    }
    return dp;
}

时间复杂度 $O(NlogN)$方法的整个过程请参看如下代码中的 lis2 方法。 

1
2
3
4
5
6
7
public int[] lis2(int[] arr) {
    if (arr == null || arr.length == 0) {
        return null;
    }
    int[] dp = getdp2(arr);
    return generateLIS(arr, dp);
}

题目八：信封嵌套问题

题目九：汉诺塔问题

题目十：最长公共子序列问题

【题目】

给定两个字符串 str1 和 str2，返回两个字符串的最长公共子序列。

【举例】

str1=”1A2C3D4B56”， str2=”B1D23CA45B6A”。

“123456”或者”12C4B6”都是最长公共子序列，返回哪一个都行。

【难度】

【解答】

本题是非常经典的动态规划问题，先来介绍求解动态规划表的过程。如果 str1 的长度为 M，str2 的长度为 N，生成大小为M×N 的矩阵 dp，行数为 M，列数为 N。 dp[i][j]的含义是 str1[0..i]与 str2[0..j]的最长公共子序列的长度。从左到右，再从上到下计算矩阵 dp。

1． 矩阵 dp 第一列即 dp[0..M-1][0]， dp[i][0]的含义是 str1[0..i]与 str2[0]的最长公共子序列长度。str2[0]只有一个字符，所以 dp[i][0]最大为 1。如果 str1[i]=str2[0]，令 dp[i][0]=1，一旦 dp[i][0]被设置为 1，之后的 dp[i+1..M-1][0]也都为 1。比如， str1[0..M-1]=”ABCDE”， str2[0]=”B”。 str1[0]为”A”， 与 str2[0]不相等，所以 dp[0][0]=0。 str1[1]为”B”， 与 str2[0]相等，所以 str1[0..1]与 str2[0]的最长公共子序列为”B”，令 dp[1][0]=1。之后的 dp[2..4][0]肯定都是 1，因为 str[0..2]、 str[0..3]和str[0..4]与 str2[0]的最长公共子序列肯定有”B”。

2． 矩阵 dp 第一行即 dp[0][0..N-1]与步骤 1 同理， 如果 str1[0]=str2[j]， 则令 dp[0][j]=1， 一旦
dp[0][j]被设置为 1，之后的 dp[0][j+1..N-1]也都为 1。

3． 对其他位置(i,j)， dp[i][j]的值只可能来自以下三种情况。

  • 可能是 dp[i-1][j]，代表 str1[0..i-1]与 str2[0..j]的最长公共子序列长度。比如， str1=”A1BC2”，
    str2=”AB34C”。str1[0..3] （ 即”A1BC”）与 str2[0..4] （ 即”AB34C”）的最长公共子序列为”ABC”，
    即 dp[3][4]为 3。 str1[0..4]（ 即”A1BC2”） 与 str2[0..4]（ 即”AB34C”） 的最长公共子序列
    也是”ABC”，所以 dp[4][4]也为 3。
  • 可能是 dp[i][j-1]，代表 str1[0..i]与 str2[0..j-1]的最长公共子序列长度。比如，str1=”A1B2C”，str2=”AB3C4”。 str1[0..4]（ 即”A1B2C”） 与 str2[0..3]（ 即”AB3C”） 的最长公共子序列为”ABC”，即dp[4][3]为 3。 str1[0..4]（ 即”A1B2C”） 与 str2[0..4]（ 即”AB3C4”）的最长公共子序列也是”ABC”，所以dp[4][4]也为 3。
  • 如果 str1[i]=str2[j]，还可能是 dp[i-1][j-1]+1。比如 str1=”ABCD”， str2=”ABCD”。 str1[0..2]
    （ 即”ABC”） 与 str2[0..2]（ 即”ABC”） 的最长公共子序列为”ABC”， 即 dp[2][2]为 3。因为str1[3]=str2[3]=”D”，所以 str1[0..3]与 str2[0..3]的最长公共子序列是”ABCD”。

上面是书中的解法，下面是leetcode的官方题解，好理解一些：

分为两种情况，str1[i]==str2[j]和str1[i]!=str2[j]:

  • str1[i]==str2[j]

    这时dp[i][j]=dp[i-1][j-1]

  • str1[i]!=str2[j]

    • 要么dp[i][j]=dp[i-1][j]
    • 要么dp[i][j]=dp[i][j-1]

    两种情况都有可能，所以取这两个中结果大的这一个，也就是max(dp[i-1][j], dp[i][j-1]).

这三个可能的值中，选最大的作为 dp[i][j]的值。具体过程请参看如下代码中的 getdp 方法。

所以这个是三个中最大的还是两个中最大的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int[][] get(char[] str1, char[] str2) {
    int[][] dp = new int [str1.length][str2.length];
    dp[0][0] = str1[0] == str2[0] ? 1 : 0;
    for (int i = 1; i < str1.length; i++) {
        dp[i][0] = Math.max(dp[i - 1][0], str1[i] == str2[0] ? 1 : 0);
    }
    for (int j = 1; j < str2.length; j++) {
        dp[0][j] = Math.max(dp[0][j - 1], str1[0] == str2[j] ? 1 : 0);
    }
    for (int i = 1; i < str1.length; i++) {
        for (int j = 1; j < str2.lenght; j++) {
            dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            if (str1[i] == str2[j]) {
                dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - 1] + 1);
            }
        }
    }
    return dp;
}

代码中是按照左程云的想法实现的。

dp 矩阵中最右下角的值代表 str1 整体和 str2 整体的最长公共子序列的长度。通过整个 dp 矩阵的状态，可以得到最长公共子序列。具体方法如下：

1． 从矩阵的右下角开始，有三种移动方式： 向上、向左、向左上。假设移动的过程中， i 表示此时的行数， j 表示此时的列数，同时用一个变量 res 来表示最长公共子序列。

2． 如果 dp[i][j]大于 dp[i-1][j]和 dp[i][j-1]，说明之前在计算 dp[i][j]的时候，一定是选择了决策 dp[i-1][j-1]+1，可以确定 str1[i]等于 str2[j]，并且这个字符一定属于最长公共子序列，把这个字符放进 res，然后向左上方移动。

3． 如果 dp[i][j]等于 dp[i-1][j]，说明之前在计算 dp[i][j]的时候， dp[i-1][j-1]+1 这个决策不是必须选择的决策，向上方移动即可。

4． 如果 dp[i][j]等于 dp[i][j-1]，与步骤 3 同理，向左方移动。

5． 如果 dp[i][j]同时等于 dp[i-1][j]和 dp[i][j-1]，向上还是向下无所谓，选择其中一个即可，反正不会错过必须选择的字符。

也就是说， 通过 dp 求解最长公共子序列的过程就是还原出当时如何求解 dp 的过程，来自哪个策略， 就朝哪个方向移动。全部过程请参看如下代码中的 lcse 方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public String lcse(String str1, String str2) {
    if (str1 == null || str2 == null || str1.equals("") || str2.equals("")) {
        return "";
    }
    char[] chs1 = str1.toCharArray();
    char[] chs2 = str2.toCharArray();
    int[][] dp = getdp(chs1, chs2);
    int m = chs1.length - 1;
    int n = chs2.length - 1;
    char[] res = new char[dp[m][n]];
    int index = res.length - 1;
    while (index >= 0) {
        if (n > 0 && dp[m][n] == dp[m][n - 1]) {
            n--;
        } else if (m > 0 && dp[m][n] == dp[m - 1][n]) {
            m--;
        } else {
            res[index--] = chs1[m];
            m--;
            n--;
        }
    }
    return String.valueOf(res);
}

计算 dp 矩阵中的某个位置就是简单比较相关的 3 个位置的值而已，所以时间复杂度为 O(1)，动态规划表 dp 的大小为 M×N，所以计算 dp 矩阵的时间复杂度为 O(M×N)。通过 dp 得到最长公共子序列的过程为 O(M+N)，因为向左最多移动 N 个位置，向上最多移动 M 个位置，所以总的时间复杂度为 O(M×N)，额外空间复杂度为 O(M×N)。如果题目不要求返回最长公共子序列，只想求最长公共子序列的长度 ，那么可以用空间压缩的方法将额外空间复杂度减小为O(min{M,N})。 有兴趣的读者请阅读本书“矩阵的最小路径和”问题，这里不再详述。

题目十一：最长公共子串问题

【题目】

给定两个字符串 str1 和 str2，返回两个字符串的最长公共子串。

【举例】

str1=”1AB2345CD”， str2=”12345EF”， 返回”2345”。

最长公共子串和最长公共子序列的区别是子串必须得连续，而子序列不必连续

【要求】

如果 str1 长度为 M， str2 长度为 N，实现时间复杂度为 O(M×N)，额外空间复杂度为 O(1)的方法。

【难度】

【解答】

经典动态规划的方法可以做到时间复杂度为 O(M×N)，额外空间复杂度为 O(M×N)，经过优化之后的实现可以把额外空间复杂度从 O(M×N)降至 O(1)，我们先来介绍经典方法。

首先需要生成动态规划表。生成大小为 M×N 的矩阵 dp，行数为 M，列数为 N。 dp[i][j]的含义是，在必须把 str1[i]和 str2[j]当作公共子串最后一个字符的情况下，公共子串最长能有多长。比如， str1=”A1234B”， str2=”CD1234”， dp[3][4]的含义是在必须把 str1[3]（即’3’） 和 str2[4]（即 ‘3’） 当作公共子串最后一个字符的情况下，公共子串最长能有多长。这种情况下的最长公共子串为”123”，所以 dp[3][4]为 3。再如， str1=”A12E4B”， str2=”CD12F4”， dp[3][4]的含义是在必须把 str1[3]（即’E’） 和 str2[4]（即’F’） 当作公共子串最后一个字符的情况下，公共子串最长能有多长。这种情况下， 根本不能构成公共子串，所以 dp[3][4]为 0。介绍了 dp[i][j]的意义后，接下来介绍 dp[i][j]怎么求。具体过程如下：

1． 矩阵 dp 第一列即 dp[0..M-1][0]。对某一个位置(i,0)来说，如果 str1[i]=str2[0]，令 dp[i][0]=1，否则令 dp[i][0]=0。比如 str1=”ABAC”， str2[0]=”A”。 dp 矩阵第一列上的值依次为 dp[0][0]=1，dp[1][0]=0，dp[2][0]=1， dp[3][0]=0。

2． 矩阵 dp 第一行即 dp[0][0..N-1]与步骤 1 同理。对某一个位置(0,j)来说，如果 str1[0]==str2[j]，令dp[0][j]=1， 否则令 dp[0][j]=0。

3． 其他位置按照从左到右， 再从上到下来计算， dp[i][j]的值只可能有两种情况。

  • 如果 str1[i]!=str2[j]，说明在必须把 str1[i]和 str2[j]当作公共子串最后一个字符是不可能的，令 dp[i][j]=0。
  • 如果 str1[i]==str2[j]，说明 str1[i]和 str2[j]可以作为公共子串的最后一个字符，从最后一 个字符向左能扩多大的长度呢？就是 dp[i-1][j-1]的值，所以令 dp[i][j]=dp[i-1][j-1]+1。

如果 str1=”abcde”， str2=”bebcd”。计算的 dp 矩阵如下：

计算 dp 矩阵的具体过程请参看如下代码中的 getdp 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int[][] getdp(char[] str1, char[] str2) {
    int[][] dp = new int[str1.length][str2.length];
    for (int i = 0; i < str1.length; i++) {
        if (str1[i] == str2[0]) {
            dp[i][0] = 1;
        }
    }
    for (int j = 1; j < str2.length; j++) {
        if (str2[j] == str1[0]) {
            dp[0][j] = 1;
        }
    }
    for (int i = 1; i < str1.length; i++) {
        for (int j = 1; j < str2.length; j++) {
            if (str1[i] == str2[j]) {
                dp[i][j] = dp[i-1][j-1] + 1;
            }
        }
    }
    return dp;
}

生成动态规划表 dp 之后，得到最长公共子串是非常容易的。比如， 上边生成的 dp 中，最大值是 dp[3][4]==3，说明最长公共子串的长度为 3。最长公共子串的最后一个字符是 str1[3]，当然也是 str2[4]，因为两个字符一样。那么最长公共子串为从 str1[3]开始向左一共 3 字节的子串， 即 str1[1..3]，当然也是 str2[2..4]。总之，遍历 dp 找到最大值及其位置，最长公共子串自然可以得到。具体过程请参看如下代码中的 lcst1 方法，也是整个过程的主方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public lcstl(String str1, String str2) {
    if (str1 == null || str2 == null || str1.equals("") || str2.equals("")) {
        return "";
    }
    char[] chs1 = str1.toCharArray();
    char[] chs2 = str2.toCharArray();
    int[][] dp = getdp(chs1, chs2);
    int end = 0;
    int max = 0;
    for (int i = 0; i < chs1.length; i++) {
        for (int j = 0; j < chs2.length; j++) {
            if (dp[i][j] > max) {
                end = i;
                max = dp[i][j];
            }
        }
    }
    return str1.substring(end - max + 1, end + 1);
}

经典动态规划的方法需要大小为 M×N 的 dp 矩阵，但实际上是可以减小至 O(1)的，因为我们注意到计算每一个 dp[i][j]的时候，最多只需要其左上方 dp[i-1][j-1]的值，所以按照斜线方向来计算所有的值，只需要一个变量就可以计算出所有位置的值，如下图所示。

每一条斜线在计算之前生成整型变量 len， len 表示左上方位置的值，初始时 len=0。从斜线最左上的位置开始向右下方依次计算每个位置的值，假设计算到位置（i,j），此时 len 表示位置（i-1,j-1） 的值。如果 str1[i]==str2[j]，那么位置（i,j） 的值为 len+1，如果 str1[i]!=str2[j]，那么位置（i,j） 的值为 0。计算后将 len 更新成位置（i,j） 的值，然后计算下一个位置，即（i+1,j+1） 位置的值。依次计算下去就可以得到斜线上每个位置的值，然后算下一条斜线。用全局变量 max 记录所有位置的值中的最大值。最大值出现时，用全局变量 end 记录其位置即可。具体过程请参看如下代码中的 lcst2 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public lcst2(String str1, String str2) {
    if (str1 == null || str2 == null || str1.equals("") || str2.equals("")) {
        return "";
    }
    char[] chs1 = str1.toCharArray();
    char[] chs1 = str1.toCharArray();
    int row = 0;  // 斜线开始位置的行
    int col = chs2.length - 1;  // 斜线开始位置的列
    int max = 0;  // 记录最大长度
    int end = 0;  // 最大长度更新时，记录子串的结尾位置
    while (row < chs1.length) {
        int i = row;
        int j = col; 
        int len = 0;
        // 从(i，j)开始向右下方遍历
        while (i < chs1.length && j < chs2.length) {
            if (chs1[i] != chs2[j]) {
                len = 0;
            } else {
                len++;
            }
            // 记录最大值，以及结束字符的位置
            if (len > max) {
                end = i;
                max = len;
            }
            i++;
            j++;
        }
        if (col > 0) {  // 斜线开始位置的列先向左移动
            col--;
        } else {  // 列移动到最左之后，向下移动
            row++;
        }
    }
    return str1.substring(end - max + 1, end + 1);
}

题目十二：子数组异或和为0的最多划分

【题目】

数组异或和的定义：把数组中所有的数异或起来得到的值。

给定一个整型数组 arr，其中可能有正、有负、有零。你可以随意把整个数组切成若干个不相容的子数组，求异或和为 0 的子数组最多能有多少个？

【举例】

arr = {3,2,1,9,0,7,0,2,1,3}

把数组分割成{3,2,1}、 {9}、 {0}、 {7}、 {0}、 {2,1,3}是最优分割，因为其中{3,2,1}、 {0}、 {0}、 {2,1,3}这四个子数组的异或和为 0，并且是所有的分割方案中，能切出最多异或和为 0 的子数组的方案， 返回 4。

【要求】

如果 arr 长度为 N，时间复杂度 O(N)。

【难度】

【解答】

本题利用动态规划，假设 arr 长度为 N，生成长度为 N 的数组 dp[]。 dp[i]的含义是如果在arr[0..i]上做分割，异或和为 0 的子数组最多能有多少个。如果可以从左到右依次求出 dp[0]、dp[1]…dp[i-1]、 dp[i]..dp[N-1]。那么 dp[N-1]的值就是： 如果在 arr[0..N-1]上做分割，异或和为 0 的子数组最多能有多少个，也就是最终答案。

现在假设 dp[0]dp[i-1]已经求出，如何求出 dp[i]就是最关键的问题。为了分析这个问题，我们假设 arr[0i]上存在最优分割。显而易见的是，分割出来的最后一个子数组一定包含 arr[i]，那么这个最优分割的最后一个子数组只可能有如下两种情况。

1）最优分割的最后一个子数组，异或和不等于 0。

2）最优分割的最后一个子数组，异或和等于 0。

对于情况 1），如果最优分割的最后一个子数组异或和不等于 0，那么 dp[i]的值等于 dp[i-1]。可以这样来理解这个结论，既然在 arr[0..i]上做最优分割，并且切出来的异或和为 0 的子数组和arr[i]没有关系，那么 arr[0..i-1]最多能切多少个， arr[0..i]上就能切多少个。

对于情况 2），如果最优分割的最后一个子数组异或和等于 0。假设 arr[k..i]就是最优分割的最后一个子数组，并且异或和等于 0，那么 dp[i]的值等于 dp[k-1]+1。可以这样理解这个结论，如果我们已经知道在 arr[0..i]上的最优分割，并且最后一个分割出的子数组是 arr[k..i]， 也知道arr[k..i]的异或和是 0。那么在 arr[0..i]上最多能分割出几个异或和为0的子数组呢？就是arr[0..k-1]上最多能够分割出的数量（dp[k-1]），再加上 arr[k..i]这部分，就是答案， dp[i] = dp[k-1] + 1。那么如何求出 k 这个位置，就变成了唯一需要关心的问题。

在 arr[0..i]上的最优分割中， 如果最后一个子数组异或和等于 0，且 arr[k..i]就是最后一个子数组。那么 k 到 i 之间的任何一个位置 j（k<j<i），都不可能有 arr[j..i]的异或和等于 0。这是因为，如果 arr[k..i]的异或和为 0，中间如果还存在一个 j 位置，使得 arr[j..i]==0，那么就可以推出 arr[k..j-1]的异或和也为 0。这样， arr[k..i]就可以分割出 arr[k..j-1]和 arr[j..i]两部分，那么岂不是比原来我们假设的最优分割更优？推出的结论与假设矛盾，所以 k 到 i 之间的任何一个位置 j（k<j<i） 都不可能有 arr[j..i]的异或和等于 0。那我们就知道 k 位置怎么求了，在 i 位置的左边所有位置中， k 一定是离 i 最近且 arr[k..i]异或和为 0 的位置。 对于其他的任何位置 j，如果也能让arr[j..i]的异或和为 0，那么 j 位置离 i 位置的距离一定比 k 位置离 i 位置的距离远。问题得到了进一步转化，现在我们关心：如果来到 i 位置，怎么求离 i 位置最近的 k 位置，使得 arr[k..i]异或和为 0。

如果我们记下 arr[0..0]的异或和、 arr[0..1]的异或和……arr[0..i-1]的异或和。现在来到 i 位置，并且arr[0..i]的异或和为 eor，我们只要知道 eor 上一次出现在什么位置，也就求出了 k 位置。
举个例子：

arr = { 6, 3, 2, 1}

位置: 0 1 2 3

展示一下来到 i==3 位置时，怎么求 k 位置。

先准备一张表 map， key：某一个异或和； value： key 这个异或和上次出现的位置。提前在 map 里放入一条记录（key = 0, value = -1），表示没遍历 arr 之前，就有 0 这个异或和。遍历到 0 位置时， arr[0..0]的异或和为 6，把（6,0） 这个记录放入 map。

此时 map 为：

（key = 0， value = -1）
（key = 6， value = 0）

遍历到 1 位置时， arr[0..1]的异或和为 5，把（ 5,1） 这个记录放入 map。此时 map 为：

（key = 0， value = -1）
（key = 6， value = 0）
（key = 5， value = 1）

遍历到 2 位置时， arr[0..2]的异或和为 7，把（ 7,2） 这个记录放入 map。此时 map 为：

（key = 0， value = -1）
（key = 6， value = 0）
（key = 5， value = 1）
（key = 7， value = 2）

遍历到 3 位置时， arr[0..3]的异或和为 6。怎么求 k？在 map 中看异或和为 6 上次出现的位置，是 0 位置。所以知道 arr[1..3]就是 arr[k..i]， 1 位置就是 k 位置。

情况 2）的分析结束。 dp[i] = dp[k-1] + 1， k 为在 i 位置左边，离 i 位置最近的使得 arr[k..i]的异或和为 0 的位置。

两种情况中哪一个值更大，哪一个就是 dp[i]的值，即 dp[i] = Max { dp[i-1], dp[k-1] + 1}。

全部流程请看 mostEOR 方法： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int mostEOR(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    int eor = 0;
    int[] dp = new int[arr.length];
    HashMap<Integer, Integer> map = new HashMap<>();
    map.put(0, -1);
    dp[0] = arr[0] == 0 ? 1 : 0;
    map.put(arr[0], 0);
    for (int i = 1; i < arr.length; i++) {
        eor ^= arr[i];
        if (map.containsKey(eor)) {
            int preEorIndex = map.get(eor);
            dp[i] = preEorIndex == -1 ? 1 : (dp[preEorIndex] + 1);
        }
        dp[i] = Math.max(dp[i - 1], dp[i]);
        map.put(eor, i);
    }
    return dp[dp.length - 1];
}

【总结】

这个动态规划的难点在于为什么arr[0…i]的异或和等于arr[0…k]的异或和时，就能推出arr[i+1…k]的异或和为0，（其中 k > i）

异或的性质

性质

1、交换律 $A \oplus B = B \oplus A$

2、结合律 $ A \oplus B \oplus C = A \oplus (B \oplus C)$

3、对于任何数x，都有$ X \oplus X = 0, X \oplus 0 = X$

4、自反性$ A \oplus B \oplus B = A \oplus 0 = A $

如果令arr[0…i]的异或和为A，arr[i+1…K]的异或和为B，那么上面的问题就可以抽象为：

已知 $ A = x, A \oplus B = x $​, 求 $B=？$

即 $ x \oplus B = x $

所以 $ B = 0 $

题目十三：最小编辑代价

【题目】

给定两个字符串 str1 和 str2，再给定三个整数 ic、 dc 和 rc， 分别代表插入、删除和替换一个字符的代价，返回将 str1 编辑成 str2 的最小代价。

【举例】

str1=”abc”， str2=”adc”， ic=5， dc=3， rc=2。

从”abc”编辑成”adc”，把’b’替换成’d’是代价最小的， 所以返回 2。

str1=”abc”， str2=”adc”， ic=5， dc=3， rc=100。

从”abc”编辑成”adc”，先删除’b’， 然后插入’d’是代价最小的， 所以返回 8。

str1=”abc”， str2=”abc”， ic=5， dc=3， rc=2。

不用编辑了，本来就是一样的字符串， 所以返回 0。

【难度】

【解答】

如果 str1 的长度为 M， str2 的长度为 N，经典动态规划的方法可以达到时间复杂度为O(M×N)，额外空间复杂度为O(M×N)。如果结合空间压缩的技巧， 可以把额外空间复杂度减至O(min{M,N})。

先来介绍经典动态规划的方法。首先生成大小为(M+1)×(N+1)的矩阵 dp， dp[i][j]的值代表str1[0..i-1]编辑成str2[0..j-1]的最小代价。举个例子， str1=”ab12cd3”， str2=”abcdf”， ic=5， dc=3，rc=2。 dp 是一个 8×6 的矩阵，最终计算结果如下。

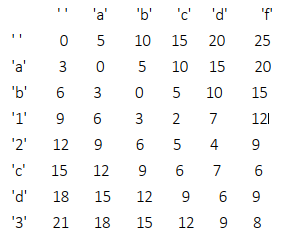
下面具体说明 dp 矩阵每个位置的值是如何计算的。

1． dp[0][0]=0，表示 str1 空的子串编辑成 str2 空的子串的代价为 0。

2． 矩阵 dp 第一列即 dp[0..M-1][0]。 dp[i][0]表示 str1[0..i-1]编辑成空串的最小代价，毫无疑问， 是把 str1[0..i-1]所有的字符删掉的代价，所以 dp[i][0]=dc * i。

3． 矩阵 dp 第一行即 dp[0][0..N-1]。 dp[0][j]表示空串编辑成 str2[0..j-1]的最小代价，毫无疑问， 是在空串里插入 str2[0..j-1]所有字符的代价，所以 dp[0][j]=ic * j。

4． 其他位置按照从左到右， 再从上到下来计算， dp[i][j]的值只可能有以下四种情况。

  • str1[0..i-1]可以先编辑成 str1[0..i-2]，也就是删除字符 str1[i-1]，然后由 str1[0..i-2]编辑成 str2[0..j-1]， dp[i-1][j]表示 str1[0..i-2]编辑成 str2[0..j-1]的最小代价，那么 dp[i][j]可能
    等于 dc+dp[i-1][j]。
  • str1[0..i-1]可以先编辑成 str2[0..j-2]，然后将 str2[0..j-2]插入字符 str2[j-1]， 编辑成str2[0..j-1]， dp[i][j-1]表示 str1[0..i-1]编辑成 str2[0..j-2]的最小代价，那么 dp[i][j]可能等于 dp[i][j-1]+ic。
  • 如果 str1[i-1]!=str2[j-1]。先把 str1[0..i-1]中 str1[0..i-2]的部分变成 str2[0..j-2]，然后把字符 str1[i-1]替换成 str2[j-1]，这样 str1[0..i-1]就编辑成 str2[0..j-1]了。 dp[i-1][j-1]表示str1[0..i-2]编辑成 str2[0..i-2]的最小代价，那么 dp[i][j]可能等于 dp[i-1][j-1]+rc。
  • 如果 str1[i-1]==str2[j-1]。先把 str1[0..i-1]中 str1[0..i-2]的部分变成 str2[0..j-2]，因为此时
    字符 str1[i-1]等于 str2[j-1]，所以 str1[0..i-1]已经编辑成 str2[0..j-1]了。 dp[i-1][j-1]表示
    str1[0..i-2]编辑成 str2[0..i-2]的最小代价，那么 dp[i][j]可能等于 dp[i-1][j-1]。

5． 以上四种可能的值中，选最小值作为 dp[i][j]的值。 dp 最右下角的值就是最终结果。具体过程请参看如下代码中的 minCost1 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public int minCost1(String str1, String str2, int ic, int dc, int rc) {
    if (str1 == null || str2 == null) {
        return 0;
    }
    char[] chs1 = str1.toCharArray();
    char[] chs2 = str2.toCharArray();
    int row = chs1.length + 1;
    int col = chs2.length + 1;
    int[][] dp = new int[row][col];
    dp[0][0] = 0;
    for (int i = 1; i < dp.length; i++) {
        dp[i][0] = i * ic;
    }
    for (int j = 1; j < dp[0].length; j++) {
        dp[0][j] = j * ic;
    }
    for (int i = 1; i < dp.length; i++) {
        for (int j = 1; j < dp[0].length; j++) {
            dp[i][j] = chs1[i - 1] == chs2[j - 1] ? (dp[i - 1][j - 1]) : (dp[i - 1][j - 1] + rc);
            dp[i][j] = Math.min(dp[i][j], dp[i][j - 1] + ic);
            dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + dc);
        }
    }
    return dp[row - 1][col - 1];

}

本题可以用空间压缩的方法将空间复杂度压缩在O（min{M, N}）, 这里不再探究。

【总结】

这道题看起来很难实际上理解了题意之后并不复杂，dp表当前位置的编辑代价dp[i][j]的值与dp表中的三个位置有关（见下图）：

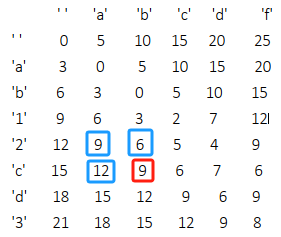
可将dp表中的每一个位置都代表一个完美编辑代价，我们想要的目的编辑代价是在其它的完美编辑代价的基础上得到的。

假设修改前的串叫材料串，修改后的串叫成品串

  • 红色框上面的蓝色框和红色框有相同长度的成品串。而蓝色框的材料串比红色框的材料串少一位，因此，从蓝色框到红色框要加上插入一个字符的代价。
  • 红色框左边的蓝色框和红色框有相同长度的材料串。而蓝色框的成品串比红色框的成品串少一为，因此，从蓝色框到红色框要加上删除一个字符的代价。
  • 红色框左上角的蓝色框与比红色框相比，材料串和成品串都少一位，此时又分为两种情况：
    • 如果 str1.charAt(i - 1) == str2.charAt(j - 1) 位置上的字符，那么蓝色框代价和红色框代价相同，因为两个字符串的最后一位相同，不需要修改了。
    • 如果 str1.charAt(i - 1) != str2.charAt(j - 1) 位置上的字符，那么蓝色框代价加上一个替换的代价才和红色框代价相同，因为两个字符串的最后一位不同，需要修改一次。

题目十四：字符串的交错组成

【题目】

给定三个字符串 str1、 str2 和 aim， 如果 aim 包含且仅包含来自 str1 和 str2 的所有字符，而且在 aim 中属于 str1 的字符之间保持原来在 str1 中的顺序，属于 str2 的字符之间保持原来在 str2 中的顺序，那么称 aim 是 str1 和 str2 的交错组成。实现一个函数，判断 aim 是否是 str1 和 str2 交错组成。

【举例】

str1=”AB”， str2=”12”。那么”AB12”、 “A1B2”、 “A12B”、 “1A2B”和”1AB2”等都是 str1 和 str2 的交错组成。

【难度】

【解答】

如果 str1 的长度为 M， str2 的长度为 N，经典动态规划的方法可以达到时间复杂度为 O(M×N)，额外空间复杂度为 O(M×N)。如果结合空间压缩的技巧， 可以把额外空间复杂度减至 O(min{M,N})。

先来介绍经典动态规划的方法。首先， aim 如果是 str1 和 str2 的交错组成， aim 的长度一定是 M+N，否则直接返回 false。然后生成大小为(M+1)×(N+1)布尔类型的矩阵 dp， dp[i][j]的值代表aim[0..i+j-1]能否被 str1[0..i-1]和str2[0..j-1]交错组成。计算 dp 矩阵的时候，是从左到右， 再从上到下计算的， dp[M][N]也就是 dp 矩阵中最右下角的值，表示 aim 整体能否被 str1 整体和 str2 整体交错组成，也就是最终结果。 下面具体说明 dp 矩阵每个位置的值是如何计算的。

1． dp[0][0]=true。 aim 为空串时，当然可以被 str1 为空串和 str2 为空串交错组成。

2． 矩阵 dp 第一列即 dp[0..M-1][0]。 dp[i][0]表示 aim[0..i-1]能否只被 str1[0..i-1]交错组成。如果 aim[0..i-1]等于 str1[0..i-1]，则令 dp[i][0]=true，否则令 dp[i][0]=false。

3． 矩阵 dp 第一行即 dp[0][0..N-1]。 dp[0][j]表示 aim[0..j-1]能否只被 str2[0..j-1]交错组成。如
果 aim[0..j-1]等于 str1[0..j-1]，则令 dp[i][0]=true，否则令 dp[i][0]=false。

4． 对其他位置(i,j)， dp[i][j]的值由下面的情况决定。

  • dp[i-1][j]代表 aim[0..i+j-2]能否被 str1[0..i-2]和 str2[0..j-1]交错组成，如果可以，那么如果再有 str1[i-1]等于 aim[i+j-1]，说明 str1[i-1]又可以作为交错组成 aim[0..i+j-1]的最后一个字符。令 dp[i][j]=true。
  • dp[i][j-1]代表 aim[0..i+j-2]能否被 str1[0..i-1]和 str2[0..j-2]交错组成，如果可以，那么如果再有 str2[j-1]等于 aim[i+j-1]，说明 str1[j-1]又可以作为交错组成 aim[0..i+j-1]的最后一个字符。令 dp[i][j]=true。
  • 如果第 1 种情况和第 2 种情况都不满足，令 dp[i][j]=false。

具体过程请参看如下代码中的 isCross1 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public boolean isCross1(String str1, String str2, String aim) {
    if (str1 == null || str2 == null || aim == null) {
        return false;
    }
    char[] ch1 = str1.toCharArray();
    char[] ch2 = str2.toCharArray();
    char[] chaim = aim.toCharArray();
    if (chaim.length != ch1.length + ch2.length) {
        return false;
    }
    boolean[][] dp = new boolean[ch1.length + 1][ch2.length + 1];
    dp[0][0] = true;
    for (int i = 1; i <= ch1.length; i++) {
        if (ch1[i - 1] != chaim[i - 1]) break;
        dp[i][0] = true;
    }
    for (int j = 1; j <= ch2.lenght; j++) {
        if (ch2[j - 1] != chaim[j - 1]) break;
        dp[0][j] = true;
    }
    for (int i = 1; i <= ch1.length; i++) {
        for (int j = 1; j <= ch2.length; j++) {
            if (dp[i - 1][j] && ch1[i - 1] == chaim[i + j - 1] || dp[i][j - 1] && ch2[j - 1] == chaim[i + j - 1]) {
                return true;
            } 

        }
    }
    return dp[ch1.length][ch2.length];
}

空间压缩的方法这里暂不做讨论。

题目十五：龙与地下城游戏问题

【题目】

给定一个二维数组 map，含义是一张地图，例如，如下矩阵：

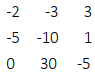
游戏的规则如下：

  • 骑士从左上角出发，每次只能向右或向下走，最后到达右下角见到公主。
  • 地图中每个位置的值代表骑士要遭遇的事情。如果是负数，说明此处有怪兽，要让骑士损失血量。如果是非负数，代表此处有血瓶，能让骑士回血。
  • 骑士从左上角到右下角的过程中，走到任何一个位置时， 血量都不能少于 1。

为了保证骑士能见到公主，初始血量至少是多少？根据 map，返回初始血量。

【相关题目】

leetcode 174.地下城游戏

【难度】

【解答】

先介绍经典动态规划的方法，定义和地图大小一样的矩阵， 记为 dp， dp[i][j]的含义是如果骑士要走上位置（i,j）， 并且从该位置选一条最优的路径， 最后走到右下角，骑士起码应该具备的血量。根据 dp 的定义， 我们最终需要的是 dp[0][0]的结果。以题目的例子来说， map[2][2]的值为-5，所以骑士若要走上这个位置， 需要 6 点血才能让自己不死。同时位置（2,2） 已经是最右下角的位置， 即没有后续的路径，所以 dp[2][2]==6。

那么 dp[i][j]的值应该怎么计算呢？

骑士还要面临向下还是向右的选择， dp[i][j+1]是骑士选择当前向右走并最终达到右下角的血量要求。同理， dp[i+1][j]是向下走的要求。如果骑士决定向右走，那么骑士在当前位置加完血或者扣完血之后的血量只要等于 dp[i][j+1]即可。 骑士在加血或扣血之前的血量要求（也就是在没有踏上（i,j） 位置之前的血量要求），就是 dp[i][j+1]-map[i][j]。同时，骑士血量要随时不少于 1，所以向右的要求为 max{dp[i][j+1]-map[i][j],1}。如果骑士决定向下走，分析方式相同，向下的要求为 max{dp[i+1][j]-map[i][j],1}。

骑士可以有两种选择，当然要选最优的一条，所以 dp[i][j]=min{向右的要求,向下的要求}。计算 dp 矩阵时从右下角开始计算，选择依次从右至左， 再从下到上的计算方式即可。

具体请参看如下代码中的 minHP1 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public int minHP1(int[][] m) {
    if (m == null || m.length == 0 || m[0] == null || m[0].length == 0) {
        return 1;
    }
    int row = m.length;
    int col = m[0].length;
    int[][] dp = new int[row--][col--];
    dp[row][col] = m[row][col] > 0 ? 1 : -m[row][col];
    for (int j = col - 1; j >=0; j--) {
        dp[row][j] = Math.max(dp[row][j + 1] - m[row][j], 1);
    }
    int right = 0;
    int down = 0;
    for (int i = row - 1; i >= 0; i--) {
        dp[i][col] = Math.max(dp[i + 1][col] - m[i][col], 1);
        for (int j = col - 1; j >= 0; j--) {
            right = Math.max(dp[i][j + 1] - m[i][j], 1);
            down = Math.max(dp[i + 1][j] - m[i][j], 1);
            dp[i][j] = Math.min(right, down);
        }
    }
    return dp[0][0];
}

我自己在leetcode中写的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int calculateMinimumHP(int[][] dungeon) {
    int m = dungeon.length;
    int n = dungeon[0].length;
    int[][] dp = new int [m][n];
    dp[m - 1][n - 1] = Math.max(1 - dungeon[m - 1][n - 1], 1);

    for (int i = m - 2; i >= 0; i--) {
        dp[i][n - 1] = Math.max(dp[i + 1][n - 1] - dungeon[i][n - 1], 1);
    }

    for (int j = n - 2; j >= 0; j--) {
        dp[m - 1][j] = Math.max(dp[m - 1][j + 1] - dungeon[m - 1][j], 1);
    }

    for (int i = m - 2; i>=0; i--) {
        for (int j = n - 2; j>=0; j--) {
            dp[i][j] = Math.max(dp[i + 1][j] - dungeon[i][j], 1);
            dp[i][j] = Math.min(dp[i][j], Math.max(dp[i][j + 1] - dungeon[i][j], 1));
        }
    }
    return dp[0][0];
}

空间压缩的方法暂不讨论。

题目十六 数字字符串转换为字母组合的种数

【题目】

给定一个字符串 str， str 全部由数字字符组成，如果 str 中某一个或某相邻两个字符组成的子串值在 1~26 之间，则这个子串可以转换为一个字母。规定”1”转换为”A”， “2”转换为”B”， “3” 转换为”C”……”26”转换为”Z”。写一个函数，求str 有多少种不同的转换结果， 并返回种数。

【举例】

str=”1111”。

能转换出的结果有”AAAA”、 “LAA”、 “ALA”、 “AAL”和”LL”， 返回 5。

str=”01”。

“0”没有对应的字母，而”01”根据规定不可转换， 返回 0。

str=”10”。

能转换出的结果是”J”， 返回 1。

【难度】

【解答】

暴力递归的方法。假设 str 的长度为 N，先定义递归函数 p(i) (0≤i≤N）。p(i)的含义是 str[0..i-1]已经转换完毕， 而 str[i..N-1]还没转换的情况下，最终合法的转换种数有多少并返回。特别指出，p(N)表示 str[0..N-1]（也就是 str 的整体） 都已经转换完，没有后续的字符了，那么合法的转换种数为 1，即 p(N)=1。比如， str=”111123”， p(4)表示 str[0..3]（即”1111”） 已经转换完毕，具体结果是什么不重要，反正已经转换完毕并且不可变，没转换的部分是str[4..5]（即”23”），可转换的只有两种，即”BC”或”W”，所以 p(4)=2。 p(6)表示 str 整体已经转换完毕，所以 p(6)=1。

p(i)如何计算呢？只有以下四种情况。

  • 如果 i=N。根据上文对 p(N)=1 的解释，直接返回 1。
  • 如果不满足情况 1，又有 str[i]==’0’。 str[0..i-1]已经转换完毕，而 str[i..N-1]此时又以’0’开头， str[i..N-1]无论怎样都不可能合法转换，所以直接返回 0。
  • 如果不满足情况 1 和情况 2，说明 str[i]属于’1’‘9’， str[i]可以转换为’A’‘I’，那么 p(i)的值一定包含 p(i+1)的值，即 p(i)=p(i+1)。
  • 如果不满足情况 1 和情况 2，说明 str[i]属于’1’‘9’，如果又有 str[i..i+1]在”10””“26”之间， str[i..i+1]可以转换为’J’~’Z’，那么 p(i)的值一定也包含 p(i+2)的值，即 p(i)+=p(i+2)。

具体过程请参看如下代码中的 num1 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int num1 (String str) {
    if (str == null || str.equals("")) {
        return 0;
    }
    char[] chs = str.toCharArray();
    return process(chs, 0);
}
public int process(char[] chs, int i) {
    if (i == chs.length) {
        return 1;
    }
    if (chs[i] == '0') {
        return 0;
    }
    int res = process(chs, i + 1);
    if (i + 1 < chs.length && (chs[i] - '0') * 10 + chs[i + 1] - '0' < 27) {
        res += process(chs, i + 2);
    }
    return res;
}

以上过程中， p(i)最多可能会有两个递归分支 p(i+1)和 p(i+2)，一共有 N 层递归，所以时间复杂度为 O(2N)，额外空间复杂度就是递归使用的函数栈的大小， 为 O(N)。但是研究一下递归函数 p 就会发现， p(i)最多依赖 p(i+1)和 p(i+2)的值，这是可以从后往前进行顺序计算的，也就是先计算 p(N)和 p(N-1)，然后根据这两个值计算 p(N-2)，再根据 p(N-1)和 p(N-2)计算 p(N-3)，最后根据 p(1)和 p(2)计算出 p(0)即可。 类似斐波那契数列的求解过程，只不过斐波那契数列是从前往后计算的，这里是从后往前计算而已。具体过程请参看如下代码中的 num2 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int num2(String str) {
    if (str == null || str.equals("")) {
        return 0;
    }
    char[] chs = str.toCharArray();
    int cur = chs[chs.length - 1] == '0' ? 0 : 1;
    int next = 1;
    int tmp = 0;
    for (int i = chs.length - 2; i >= 0; i--) {
        if (chs[i] == '0') {
            next = cur;
            cur = 0;
        } else {
            tmp = cur;
            if ((chs[i] - '0') * 10 + chs[i + 1] - '0' < 27) {
                cur += next;
            }
            next = tmp;
        }
    }
    return cur;
}

因为是顺序计算，所以 num2 方法的时间复杂度为 O(N)，同时只用了 cur、 next 和 tmp 进行滚动更新，所以额外空间复杂度为 O(1)。但是本题并不能像斐波那契数列问题那样用矩阵乘法的优化方法将时间复杂度优化到 O(logN)，这是因为斐波那契数列是严格的 f(i)=f(i-1)+f(i-2)，但是本题并不严格， str[i]的具体情况决定了 p(i)是等于 0 还是等于 p(i+1)或 p(i+1)+p(i+2)。有状态转移的表达式不可以用矩阵乘法将时间复杂度优化到 O(logN)。但如果 str 只由字符’1’和字符’2’组成，比如”12121121212122”，那么就可以使用矩阵乘法的方法将时间复杂度优化为 O(logN)。因为 str[i] 都 可 以 单 独 转 换 成 字 母 ， str[i..i+1] 也 都 可 以 一 起 转 换 成 字 母 ， 此 时 一 定 有p(i)=p(i+1)+p(i+2)。总之，可以使用矩阵乘法的前提是递归表达式不会发生转移。

题目十七：表达式得到期望结果的组成种数

题目十八：排成一条线的纸牌博弈问题

【题目】

给定一个整型数组 arr，代表数值不同的纸牌排成一条线。玩家 A 和玩家 B 依次拿走每张纸牌， 规定玩家 A 先拿， 玩家 B 后拿， 但是每个玩家每次只能拿走最左或最右的纸牌，玩家 A 和玩家 B 都绝顶聪明。请返回最后获胜者的分数。

【举例】

arr=[1,2,100,4]。

开始时， 玩家 A 只能拿走 1 或 4。如果玩家 A 拿走 1，则排列变为[2,100,4]，接下来玩家 B可以拿走 2 或 4， 然后继续轮到玩家 A。如果开始时玩家 A 拿走 4， 则排列变为[1,2,100]，接下来玩家 B 可以拿走 1 或 100，然后继续轮到玩家 A。玩家 A 作为绝顶聪明的人不会先拿 4，因为拿 4 之后， 玩家 B 将拿走 100。所以玩家 A 会先拿 1，让排列变为[2,100,4]，接下来玩家 B 不管怎么选， 100 都会被玩家 A 拿走。玩家 A 会获胜，分数为 101。所以返回 101。

arr=[1,100,2]。

开始时， 玩家 A 不管拿 1 还是 2，玩家 B 作为绝顶聪明的人，都会把 100 拿走。玩家 B 会获胜，分数为 100。所以返回 100。

【难度】

【解答】

暴力递归的方法。定义递归函数 f(i,j)，表示如果 arr[i..j]这个排列上的纸牌被绝顶聪明的人先拿，最终能获得什么分数。定义递归函数 s(i,j)，表示如果 arr[i..j]这个排列上的纸牌被绝顶聪明的人后拿，最终能获得什么分数。

首先分析 f(i,j)，具体过程如下：

1． 如果 i==j（ 即 arr[i..j]） 上只剩一张纸牌。当然会被先拿纸牌的人拿走，所以返回 arr[i]。

2． 如果 i!=j。当前拿纸牌的人有两种选择，要么拿走 arr[i]， 要么拿走 arr[j]。如果拿走 arr[i]，那么排列将剩下 arr[i+1..j]。对当前的玩家来说，面对 arr[i+1..j]排列的纸牌，他成了后拿的人，所以后续他能获得的分数为 s(i+1,j)。如果拿走 arr[j]，那么排列将剩下 arr[i..j-1]。对当前的玩家来说，面对 arr[i..j-1]排列的纸牌，他成了后拿的人，所以后续他能获得的分数为 s(i,j-1)。作为绝顶聪明的人，必然会在两种决策中选最优的。所以返回 max{arr[i]+s(i+1,j) , arr[j]+s(i,j-1)}。

然后分析 s(i,j)，具体过程如下：

1． 如果 i==j（即 arr[i..j]） 上只剩一张纸牌。作为后拿纸牌的人必然什么也得不到，返回 0。

2． 如果 i!=j。根据函数 s 的定义，玩家的对手会先拿纸牌。对手要么拿走 arr[i]， 要么拿走arr[j]。如果对手拿走 arr[i]，那么排列将剩下 arr[i+1..j]，然后轮到玩家先拿。如果对手拿走 arr[j]，那么排列将剩下 arr[i..j-1]，然后轮到玩家先拿。对手也是绝顶聪明的人，必然会把最差的情况留给玩家。所以返回 min{f(i+1,j) , f(i,j-1)}。

具体过程请参看如下代码中的 win1 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int win1(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));
}

public int f(int[] arr, int i, int j) {
    if (i == j) {
        return arr[i];
    }
    return Math.max(arr[i] + s(arr, i + 1, j), s(arr, i, j - 1));
}

public int s(int[] arr, int i, int j) {
    if (i == j) {
        return 0;
    }
    return Math.min(f(arr, i + 1, j), f(arr, i, j - 1));
}

暴力递归的方法中，递归函数一共会有 N 层，并且是 f 和 s 交替出现的。 f(i,j)会有 s(i+1,j)和 s(i,j-1)两个递归分支， s(i,j)也会有 f(i+1,j)和 f(i,j-1)两个递归分支。所以整体的时间复杂度为O($2^N$)，额外空间复杂度为 O(N)。下面介绍动态规划的方法，如果 arr 长度为 N，生成两个大小为 N×N 的矩阵 f 和 s， f[i][j]表示函数 f(i,j)的返回值， s[i][j]表示函数 s(i,j)的返回值。规定一下两个矩阵的计算方向即可。具体过程请参看如下代码中的 win2 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int win2(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    int[][] f = new int[arr.length][arr.length];
    int[][] s = new int[arr.length][arr.length];
    for (int j = 0; j < arr.length; j++) {
        f[j][j] = arr[j];
        for (int i = j - 1; i >= 0; i--) {
            f[i][j] = Math.max(arr[i] + s[i + 1][j], arr[j] + s[i][j - 1]);
            s[i][j] = Math.min(f[i + 1][j], f[i][j - 1]);
        }
    }
    return Math.max(f[0][arr.length - 1], s[0][arr.length - 1]);
}

如上的 win2 方法中，矩阵 f 和 s 一共有 O($N^2$)个位置，每个位置计算的过程都是 O(1)的比较过程，所以 win2 方法的时间复杂度为 O($N^2$)，额外空间复杂度为 O($N^2$)。

题目十九：跳跃游戏

【题目】

给定数组 arr， arr[i]=k 代表可以从位置 i 向右跳 1~k 个距离。比如， arr[2]=3，代表可以从位置 2 跳到位置 3、 位置 4 或位置 5。如果从位置 0 出发，返回最少跳几次能跳到 arr 最后的位置上。

【举例】

arr=[3,2,3,1,1,4]。
arr[0]=3，选择跳到位置 2； arr[2]=3，可以跳到最后的位置。所以返回 2。

【要求】

如果 arr 长度为 N，要求实现时间复杂度为 O(N)、 额外空间复杂度为 O(1)的方法。

【难度】

具体过程如下：
1． 整型变量 jump，代表目前跳了多少步。整型变量 cur，代表如果只能跳 jump 步，最远能够达到的位置。整型变量 next，代表如果再多跳一步，最远能够达到的位置。初始时， jump=0，cur=0， next=0。

2． 从左到右遍历 arr，假设遍历到位置 i。

1）如果 cur≥i，说明跳 jump 步可以到达位置 i，此时什么也不做。

2）如果 cur<i，说明只跳 jump 步不能到达位置 i，需要多跳一步才行。此时令 jump++， cur=next。表示多跳了一步， cur 更新成跳 jump+1 步能够达到的位置，即 next。

3）将 next 更新成 math.max(next, i+arr[i])，表示下一次多跳一步到达的最远位置。

3． 最终返回 jump 即可。

具体过程请参看如下代码中的 jump 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int jump(int[] arr) {
    if (arr == null || arr.length == 0) {
        return 0;
    }
    int jump = 0;
    int cur = 0;
    int next = 0;
    for (int i = 0; i < arr.length; i++) {
        if (cur < i) {
            jump++;
            cur = next;
        }
        next = Math.max(next, i + arr[i]);
    }
    return jump;
}

题目二十：数组中最长连续序列

题目二一：N皇后问题

【题目】

N 皇后问题是指在 N×N 的棋盘上要摆 N 个皇后，要求任何两个皇后不同行、不同列，也不在同一条斜线上。给定一个整数 n，返回 n 皇后的摆法有多少种。

【举例】

n=1， 返回 1。
n=2 或 3， 2 皇后和 3 皇后问题无论怎么摆都不行，返回 0。
n=8， 返回 92。

【难度】

【解答】

本题是非常著名的问题，甚至可以用人工智能相关算法和遗传算法进行求解，同时可以用多线程技术达到缩短运行时间的效果。本书不涉及专项算法，仅提供在面试过程中 10 至 20 分钟内可以用代码实现的解法。本书提供的最优解做到在单线程的情况下，计算 16 皇后问题的运行时间约为 13 秒。在介绍最优解之前，先来介绍一个容易理解的解法。

如果在（i,j） 位置（第 i 行第 j 列） 放置了一个皇后，接下来在哪些位置不能放置皇后呢？

1． 整个第 i 行的位置都不能放置。

2． 整个第 j 列的位置都不能放置。

3． 如果位置（a,b） 满足|a-i|=|b-j|，说明（a,b） 与（i,j） 处在同一条斜线上，也不能放置。把递归过程直接设计成逐行放置皇后的方式，可以避开条件 1 的那些不能放置的位置。接下来用一个数组保存已经放置的皇后位置，假设数组为 record，record[i]的值表示第 i 行皇后所在的列数。在递归计算到第 i 行第 j 列时，查看 record[0..k]（k<i） 的值，看是否有 j 相等的值，若有， 则说明（i,j） 不能放置皇后，再看是否有|k-i|==|record[k]-j|， 若有， 也说明（i,j） 不能放置皇后。具体过程请参看如下代码中的 num1 方法。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public int num1(int n) {
    if (n < 1) {
        return 0;
    }
    int[] record = new int[n];
    return process1(0, record, n);
}

public int process1(int i, int[] record, int n) {
    if (i == n) {
        return 1;
    }
    int res = 0;
    for (int j = 0; j < n; j++) {
        if (isValid(record, i, j)) {
            record[i] = j;
            res += process1(i + 1, record, n);
        }
    }
    return res;
}

public boolean isValid(int[] record, int i, int j) {
    for (int k = 0; k < i; k++) {
        if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
            return false;
        }
    }
    return true;
}